Точки, линии и области

Все мы видели игры типа Asteroids, Spectre и Major Havoc. Многие из них имеют общие черты первых видеоигр — все они выполнены линиями и все они, как правило, плоские. Кстати, в предыдущих главах мы еще ничего не делали для рисования проекции кроме отображения точки.

Точки, линии, многоугольники и объекты в трехмерном пространстве

Как мы уже видели, точка в трехмерном пространстве имеет три координаты (x,y,z). Этой информации достаточно, чтобы ее однозначно определить в пространстве.Будет логично, если следующим объектом, который мы определим, станет линия. Линией называют отрезок, соединяющий две точки в трехмерном пространстве. Мы можем даже написать структуры данных, определяющие точку и линию.

Листинг 6.1. Определение точки и линии в трехмерном пространстве.

// структура, описывающая точку в трехмерном пространстве

typedef struct point_typ

{

float x,y,z // координаты точки

} point, *point_ptr;

// структура, описывающая линию в трехмерном пространстве

typedef struct line_typ

{

point start, end; // линия задается двумя точками

} line, *line_ptr;

Используя структуры из Листинга 6,1, давайте определим линию, которая начинается в точке (0,0,0) и идет в точку (100,200,300)

line linel;

linel.start.x = 0;

linel.start.у= 0;

linel.start.z = 0;

linel.end.x = 100;

linel.end.у = 200;

linel.end.z = 300;

Теперь мы имеем описание линии. Если мы захотим, то сможем создать трехмерный мир, состоящий из линий и точек, но это будет скучным и тоскливым занятием.

Нам нужен больший уровень абстракции для моделирования объектов, и для этого нам пригодятся многоугольники. Как вы поняли из четвертой главы, многоугольник - это множество вершин, соединенных отрезками прямых. Вершины определяют границы многоугольника. В трехмерном пространстве Многоугольники очень похожи на своих двухмерных собратьев. Попробуем определить трехмерный треугольник. Он может выглядеть так, как это изображено иа рисунке 6.2.

Как вы можете видеть, на листе бумаги весьма несложно представить трехмерный объект. Мы будем использовать для описания «диагональный вид». Позже,мы к этому еще вернемся, а сейчас важно понять идею.

Описать многоугольник довольно просто: мы применим старое определение многоугольника и просто добавим к нему несколько атрибутов для создания новой законченной структуры. В Листинге 6.2 показана такая структура.

Листинг 6.2. Определение трехмерного многоугольника.

// структура, описывающая многоугольник

typedef struct polygon_typ

{

int num_vertices;                 // число

вершин

vertices[MAX VERTICES];           // координаты

вершин

int color;                        // цвет многоугольника

}polygon, *polygon_ptr;

Как можно заметить, в структуре описаны вершины и цвета. Эти составляющие необходимы для правильного отображения. Теперь, когда у нас есть структура, описывающая многоугольник, следующим шагом будет определение объекта на основе многоугольников. На рисунке 6.3 продемонстрирован один из таких объектов.

Теперь мы можем добавить еще один уровень к нашему описанию. Объект - это набор многоугольников. Создадим структуру, которая бы поддерживала эту концепцию:

Листинг 6.3. Описание трехмерного объекта на основе многоугольников.

// структура, описывающая объект

typedef struct object_typ

{

int num_faces;             // число

граней

polygon faces[max_faces]; // грани, представленные многоугольниками

float xo,yo,zo;            // координаты объекта в пространстве

int visible;              // виден ли объект на экране?

} object, *object_ptr;

Структура данных в Листинге 6.3 описывает объект, который образован , множеством многоугольников или поверхностей. Используя эти структуры данных и определения, мы можем создать несколько трехмерных объектов: космический корабль, планету и окружающее космическое пространство.

Чтобы поместить объекты в трехмерное пространство, мы должны знать их пространственное расположение. То есть мы должны определить значения хо, уо и zo для каждого предмета. Так же, как и в случае с двухмерными объектами (которые мы уже обсуждали в четвертой главе), пространственные объекты мы будем определять в собственных локальных системах координат (0,0,0). Затем, когда мы будем перемещать объект, мы его просто переведем в конечную позицию.

Для наших структур это будет точка (xo,yo,zo).

Решением этой задачи будет простой перенос каждой из точек объекта, так же, как мы это делали для двухмерных объектов. Мы можем проверить этот метод и для объемных фигур. Например, представим себе куб, с вершиной в точке (2,2,2) (см. рис. 6.4). Если мы посмотрим на куб, то увидим, что он состоит из восьми вершин и шести поверхностей. Используя наши структуры данных, мы можем описать куб как объект с шестью гранями. Проблема, возникающая в данном случае, состоит в том, что это не самый лучший способ описания объекта. Ведь любая поверхность ограничена четырьмя точками и каждая из этих точек является общей еще для двух поверхностей. Это значит, что описание избыточно.

Возможно, более удачной окажется структура данных, содержащая список вершин. В этом случае избыточности не возникает. Однако при этом структура станет более общей и сложной, поскольку:

§          Мы должны будем иметь указатели либо индексы, или то и другое вместе для ссылки на вершины, необходимые для построения геометрической фигуры. Это увеличивает время распознавания данных объектов;

§          Наши структуры могут использовать заранее определенные массивы для хранения вершин и многоугольников. Это неэффективно использует память. Массивы должны быть одного размера, так как, независимо от того, используем ли мы один элемент массива или весь массив, нам необходимо отводить место под максимальное число элементов.

Эти факты надо принимать во внимание, когда создаете структуры для трехмерных объектов. Таким образом, для наших целей структуры данных из Листингов 6.2 и 6.3 являются наиболее простыми для работы. Если же вы хотите создать набор реальных трехмерных структур, то должны использовать другую тактику.

В общем случае представление двух- и трехмерных объектов сильно зависит от игры, которую вы пишете, от размера используемой памяти и т. д. (Наша цель сейчас - понять механизмы трехмерной графики и рендеринга, а не поиск наиболее эффективных способов представления данных в компьютере.

Это зависит от используемых алгоритмов и структур данных.)

Просуммируем все вышесказанное:

§                           Трехмерные объекты состоят из вершин;

§                           Эти вершины соединяются поверхностями или многоугольниками, которые задают границы объекта;

§                           Объекты описываются относительно начала координат;

§                           Существует много способов представления трехмерных объектов и вы должны выбрать тот, который устраивает вас по скорости и объему памяти.

Трансляция объектов

Трансляцией объекта будем называть его перемещение, при котором не меняется ни угол поворота, ни размер объекта. Давайте воспользуемся нашей структурой данных для определения конкретного объекта, с которым будем экспериментировать и в дальнейшем. К примеру, пусть это будет астероид. На рисунке 4.7 показан его внешний вид. Листинг 4.5 содержит фрагмент, описывающий наш астероид.

Листинг 4.5. Описание астероида.

Object asteroid;

// определим поля

asteroid.num_vertices = 6; //шести вершин будет достаточно

asteroid.color

= 1; //цвет астероида - синий

asteroid.х0 = 320; // поместить астероид в центр экрана

asteroid.у0 = 240;

//теперь задаем координаты вершин как смещения относительно точки х0, у0

asteroid.vertices[0].х = 4.0;

asteroid.vertices[0].у = 3.5;

asteroid.vertices[1].х = 8.5;

asteroid.vertices[1].у = -3.0;

asteroid.vertices[2].x = 6;

asteroid.vertices[2].у = -5;

asteroid.vertices[3],x = 2;

asteroid.vertices[3].у = -3;

asteroid.vertices[4].х = -4;

asteroid.vertices[4].у = -6;

asteroid.vertices[5].х = -3.5;

asteroid.vertices[5].у = 5.5;

Конечно, в настоящих играх вам не придется так определять все свои объекты. Напротив, вы можете загрузить координаты вершин из файла или сгенерировать их (например, AutoCad использует формат DXF, содержащий списки вершин вместе с другими свойствами объекта; после того как DXF-файл загружен, координаты вершин считываются из него в соответствующие структуры). Но поскольку мы создаем всего один астероид, то можно описать его и вручную.

Теперь давайте чуть-чуть подумаем. Мы можем нарисовать вершины объекта относительно его положения на экране, которое описывается как (хо,уо). Если же мы хотим передвинуть объект, то можно сделать так:

x0=x0+dx

y0=y0+dy

где dx и dy — это количество пикселей, на которое мы хотим переместить объект по оси Х или Y.

Это все, что можно сказать о трансляции объектов. Теперь поговорим о масштабировании.

Трассировка луней

Трассировка лучей - это метод, применяемый для создания реалистичных образов на компьютере, используя полные модели трехмерного мира. Трассировка лучей решает множество проблем. Этот алгоритм может выполнять следующие действия:

Удаление невидимых поверхностей;

§ Перемещение;

§ Отражение;

§ Рассеяние;

§ Окружающее освещение;

§ Точечное освещение;

§ Наложение теней.

Изначально этот алгоритм разрабатывался для решения проблемы удаления невидимых поверхностей. Трассировка лучей создает образ, исходя из тех же законов, что и наше зрение. На рисунке 6.19 изображено некоторое пространство, которое может быть просчитано с помощью алгоритма трассировки лучей. Вы видите несколько объектов: источник света, наблюдателя и план наблюдения.

Чтобы воспользоваться трассировкой лучей для создания натуральных образов, нам придется использовать миллиарды световых лучей из источника света, и затем рассматривать каждый из них, надеясь, что он попадет в план наблюдения и примет участие в создании образа. Возникает вопрос - а зачем трассировать каждый возможный луч? На самом деле, нас интересуют только те лучи, которые достигают плана просмотра.

Запомнив это, давайте попробуем трассировать лучи в обратном направлении. Проследим движение лучей для каждого из пикселей на экране, а затем посмотрим, где эти лучи пересекаются с планом просмотра. Отметив пересечение, мы останавливаемся и окрашиваем соответствующий пиксель в нужный цвет. Это называется первичной трассировкой лучей.

Данная техника позволяет создавать трехмерные образы, но при этом не видны такие эффекты, как тени, рефракция и рефлексия. Чтобы воссоздать перечисленные эффекты, мы должны принять в рассмотрение специальные вторичные лучи, которые исходят из точек пересечения.

Это все делается рекурсивно до достижения некоторого уровня детализации. Затем полученные по всем лучам результаты складываются и соответствующему пикселю присваивается вычисленный цвет.

Трассировка лучей - это один из наиболее насыщенных вычислениями методов расчета трехмерных изображений, но зато и результаты получаются впечатляющими. Есть только одна проблема: для решения этой задачи в реальном времени не хватает мощности даже самого быстродействующего компьютера. Потому нам придется учесть данное обстоятельство и применить идею трассировки лучей для создания другого метода. Он будет более ограничен, но позволит нормально работать с трехмерными мирами на обычном ПК. Исходя из этого, мы попробуем реализовать упрощенный вариант трассировки лучей, используя только первичные лучи для генерации изображения. С последующими оптимизациями возможно достижение достаточно высокой производительности. Если вам интересно узнать, как это можно сделать, то стоит продолжить чтение нашей книги.

Трехмерное звездное небо

Техника трехмерных спрайтов, которую мы обсуждаем, используется не только в играх типа Wing Commander, но также и в DOOM, и в Wolfenstein. Если вы поиграете в DOOM, то заметите, что гуляющие или преследующие вас монстры (спрайты) изображаются в разных видах. В шестой главе, «Третье измерение», мы обсуждали метод трассировки лучей и метод представления объектов с помощью многоугольников. Теперь я хотел бы снова вернуться к этому и показать, как можно создать трехмерное космическое пространство внутри которого и будут происходить наши звездные войны.

Теоретически создание трехмерного звездного неба тривиально. Мы могли бы просто задать несколько миллионов случайных точек в трехмерном пространстве, использовать аксонометрическую проекцию для их визуализации и, нарисовать их по пикселям. Этот метод волне применим и обычно используется в симуляторах. Однако у него есть ряд недостатков: он работает медленно, требует много памяти и получаемое в результате изображение быстро надоедает из-за своего однообразия. Но поскольку мы с вами сейчас занимаемся оформлением игры, то должны сделать так, чтобы экран действительно стал трехмерным звездным небом. Но мало сказать, надо еще и сделать! Если вы найдете время и посмотрите Star Trek или подобный симулятор, то увидите звездное небо, созданное с помощью одиночных пикселей (звезд). Эти звезды расположены на экране случайным образом и передвигаются к периферии вначале медленно, а потом все быстрее и быстрее. Это происходит до тех пор, пока звезды не будут отсечены, выйдя за пределы обозримого пространства.

Удачный угол зрения на спрайты

Эта тема наиболее сложная из всех, которые мы до сих пор рассматривали. При перемещении трехмерных спрайтов по экрану, с точки зрения наблюдателя все должно выглядеть так, словно объекты и в самом деле имеют три измерения. Наблюдатель в нашем случае — это игрок, и его позиция фиксирована. Обычно она имеет координаты (0,0,0) или слегка сдвинута по оси Z. В любом случае, когда спрайт, к примеру, делает поворот, и мы хотим, чтобы он выглядел как настоящий трехмерный объект, нам следует менять кадры этого спрайта на экране в последовательности, соответствующей реальной смене ракурсов «живого» объекта. (Такую фразу и не выговоришь на одном дыхании!)

Полное и элегантное решение этой проблемы слишком... масштабно для нас. Нам всего лишь требуется, чтобы наши программы, модели и алгоритмы. давали реалистичные результаты. Поэтому, алгоритм, который мы обсудим в этом разделе, едва ли решит поставленную задачу в полном объеме, и в будущем, вы наверняка внесете в него свои дополнения. Однако он является хорошей стартовой площадкой, а я всегда предпочитаю иметь хороший фундамент для последующего строительства, а не слабое его подобие, на котором после ничего и не соорудишь.

Как и при написании любой программы для любого компьютера, мы должны вначале четко определить задачу, а затем обдумать возможные пути ее решения. • Итак, проблема: как выбрать кадр для изображения объекта на основании угла между лучом зрения игрока и направлением «взгляда» самого объекта.

Замечание

В общем случае объект может передвигаться и не в том направлении, куда обращена его лицевая сторона, Мы не будем сейчас заострять внимание на этом варианте движения, чтобы чрезмерно не усложнять нашу задачу. Пока будем считать, что объект всегда движется в ту сторону, куда он обращен лицом. Это предположение вполне обосновано, так как в программе, которую мы впоследствии напишем, будут участвовать космические корабли с кормовыми дюзами. Точно так же и в играх типа Wolfenstein или DOOM игровые персонажи обычно движутся в том направлении, куда они смотрят (или в обратном, если они пятятся).

Попытаемся вначале проанализировать проблему. Нам необходимо определить вид объекта, который зависит от направления взгляда игрока и траектории объекта или направления его движения. Как мы уже говорили, луч зрения игрока можно зафиксировать и считать, что он всегда перпендикулярен экрану. Тогда нам нужно будет побеспокоиться только о векторе траектории объекта, выводимого на экран. На рисунке 8.7 изображена взаимосвязь между вектором направления взгляда игрока и некоторой траекторией передвижения объекта.

Теперь мы должны сделать вот что: возьмем игрушечную машинку или что-нибудь подобное и будем передвигать ее перед собой (шум мотора имитировать при этом не обязательно, можно все делать тихо). Проделав это, вы быстро придете к выводу, что рисуемое на экране изображение космического корабля, движущегося прямолинейно, практически одинаково для всех параллельных траекторий независимо от местоположения объекта. Конечно, это справедливо только частично, зато мы получили хорошую отправную точку для нашего первого алгоритма выбора правильного кадра.

Что же мы должны сделать:

§          Вычислить угол между траекторией движения объекта и лучом зрения игрока (который всегда направлен прямо в экран);

§          Разделить полученный угол на квадранты. Затем на основании полученного индекса выбрать наиболее подходящее изображение среди предварительно подготовленных оцифровкой фотографий модели или нарисованных в графическом редакторе. (Более подробно это обсуждается в разделе «Оцифровка объектов и моделирование».)

§          Вывести на экран подходящий кадр, используя аксонометрическую проекцию и масштабируя объект до необходимого размера.

В результате на экране получается реалистичная картина.

Каким же образом находится угол между траекторией объекта и лучом зрения наблюдателя? Ответ может быть получен с помощью скалярного произведения векторов.

Мы знаем, что угол между двумя векторами можно найти с помощью скалярного произведения векторов, как это показано на рисунке 8.8.

Формула 8.4. Вычисление угла между наблюдателем и объектом.

Если мы зададим вектор направления взгляда, как V, а вектор скорости, как О, тогда угол между ними можно будет найти по следующей формуле:

Пусть V = (vx,vy,vz) и О = (ox,oy,oz), тогда

Если бы мы хотели сформулировать это действие словами, то могли бы сказать так: «Угол между V и О равен арккосинусу скалярного произведения этих векторов, разделенного на произведение длин векторов».

Угол между V и О, рассчитанный по этой формуле, имеет одну особенность: он всегда внутренний, то есть больше 0, но меньше 180 градусов. Следовательно, один и тот же результат, полученный по этой формуле, может соответствовать двум разным углам. Это происходит потому, что скалярное произведение не дает информации о направлении вектора (или о направлении, в котором вы отсчитываете положительный угол). Другими словами, эта формула всегда выдает наименьший из углов между двумя векторами. Если вы будете помнить об этом, то такое поведение данной формулы не будет большой проблемой. (Это напоминает бутерброд, который всегда падает маслом вниз. Если вы не знаете об этом, то такой результат может свести вас с ума. А кто предупрежден, тот вооружен.)

Рисунок 8.9 иллюстрирует указанную проблему графически. На этом рисунке показан вектор направления взгляда, три возможных положения вектора траектории и полученный в результате расчетов по формуле 8.4 угол.

Кстати, формулу 8.4 можно значительно упростить, вспомнив, что нас интересует только плоскость X-Z, так как луч зрения всегда перпендикулярен плоскости просмотра.

Но как же, в конце концов, определить действительный угол? Конечно, вы Могли бы воспользоваться еще и векторным произведением, чтобы решить, корректен ли угол, полученный в результате расчетов по формуле 8.4 или необходимо увеличить его еще на 180 градусов. Однако я слишком не люблю математику (возможно, именно поэтому я и доктор математических наук) и предпочитаю вместо грубой силы использовать тонкую интуицию.

Если мы сообразим, что вектор траектории объекта имеет ту же исходную точку, что и вектор направления взгляда, а затем проверим, в какой из полуплоскостей относительно луча зрения расположен Х-компонент вектора траектории, то мы сможем определить, больше или меньше 180° искомый угол. Это наглядно изображено на рисунке 8.10.

Применяя метод проверки Х-компонента, мы можем написать простую функцию, которая вначале рассчитывает угол, используя скалярное произведение, а затем проверяет, находится ли координата Х справа (положительная) или слева (отрицательная) от вектора направления взгляда. Если координата Х положительная, мы вычитаем угол, полученный с помощью формулы 8.4 из 360 градусов (это все равно, что прибавить 180). Затем мы можем взять рассчитанный угол и разбить его на 12 квадрантов (либо взять его модуль по основанию 12). Полученное число затем можно использовать как индекс для нахождения кадров спрайта. (Конечно, кадры должны быть расположены в правильном порядке, то есть кадрам, полученным при вращении объекта против часовой стрелки с шагом в 30 градусов, должны соответствовать индексы от 0 до 11. При этом нулевой индекс должен указывать на кадр объекта, повернутого тыльной стороной к наблюдателю.)

Если значение координаты Х отрицательное, происходит то же самое за исключением того, что будет использован другой банк изображений, и оперировать потребуется с абсолютным значением X.

Кадры, которые я создал для демонстрации этого алгоритма, расположены в файле VRYENTXT.PCX. Они расположены слева направо и сверху вниз. Каждая картинка содержит изображение, повернутое на 30° против часовой стрелки, а в исходной позиции нос корабля направлен прямо в экран (или, с точки зрения игрока, корабль обращен к нему тыльной стороной). Этот же файл мы использовали и в предыдущем примере.

Демонстрационная программа будет использовать рассчитываемые углы для выбора кадров. Но мы же не можем поместить корабль просто в пустоту. Это будет скучно! Нам надо добавить что-нибудь для оживления картинки.Я предлагаю создать трехмерное звездное небо. Под трехмерностью я здесь понимаю то, что звезды будут перемещаться к вам или от вас, а не влево или вправо, как это мы делали раньше, Надо отметить, что космический корабль, летящий в звездном пространстве, выглядит превосходно. Однако следует еще поговорить о том, как же создается такое трехмерное звездное небо.

Удаление невидимых поверхностей

Среди программистов, работающих в области компьютерной графики, техника удаления невидимых поверхностей считается «высшим пилотажем». Известно, что удаление невидимых поверхностей является сложной математической задачей. Существует довольно много алгоритмов для ее решения, но все они очень сложны в реализации и редко работают с приемлемой для видеоигр скоростью.

Удаление невидимых поверхностей можно разделить на две фазы:

Фаза 1. Прежде всего удаляются поверхности, которые никогда не будут видны с точки зрения наблюдателя. Для этого мы должны использовать точку пересечения между вектором наблюдения и вектором нормали к каждой из рассматриваемых плоскостей. Мы вычисляем это значение. Если значение угла меньше 90°, то поверхность видна, если больше 90° - нет и она удаляется.

Фаза 2. После того как скрытые поверхности удалены, видимые плоскости должны быть окрашены. Вы должны быть уверены, что в течение этой фазы, объекты будут выглядеть правильно.

Существует популярный Алгоритм Художника, который это хорошо умеет делать. Он работает, выполняя пять тестов для каждой видимой пары многоугольников (поверхностей) и затем создает последовательность их окраски от дальней части изображения к ближней.

Другая техника создания этой последовательности носит название Алгоритма Z-буфера. Он работает в пространстве образа на уровне пикселей. Он прост в реализации, но медленно работает и требует много памяти.

Настоящие разработчики видеоигр никогда не используют эти алгоритмы в чистом виде. Мы должны создать свою систему», которая будет сочетать оба метода. Для этого детально рассмотрим каждый из них.

Удобные детали и инструменты

На что вам в первую очередь необходимо обратить внимание при выборе графической программы? Существует не так уж и много возможностей графических редакторов, которые я использую наиболее часто. Я с удовольствием помогу вам и укажу на них:

Посмотрите, есть ли в программе возможность импорта и экспорта различных графических форматов. Существует целое семейство битовых графических форматов, и у вас должна иметься возможность отконвертировать любое изображение в тот формат, который вы в конечном счете используете. К примеру, вы можете решить, что ваши окончательные картинки должны сохраняться в PCX-файлах, но нашли несколько интересных изображений в GIF-, BMP- или TIF-формате. Было бы прекрасно иметь возможность преобразовать их в выбранный формат, при необходимости отредактировать и сохранить в новом PCX-файле. Эти четыре формата наиболее часто употребляются графическими редакторами, поддерживающими 256-цветный режим;

§ Обратите внимание на способ управления цветами и их расположение в палитре. У вас может возникнуть необходимость собрать окончательное изображение из нескольких исходных картинок, и вам потребуется создать палитру, которая будет обеспечивать наилучшие результаты с различными типами изображений. Вы можете обнаружить, что комбинирование этих изображений приводит к перемешиванию палитры. Возможность перестановки цветов по яркости оттенков является удобной деталью. Мы еще вернемся к этой возможности и рассмотрим ее чуть позже в данной главе;

§ Очень хорошо, если программа позволяет уменьшить количество цветов в изображении. Вы быстро обнаружите, что 256 цветов вам хватит ненадолго, если вы работаете с несколькими фотографиями или набором текстур. Вам может потребоваться уменьшить количество цветов, используемое каждым изображением, до 64 или даже до 32;

§          Очень хорошей особенностью некоторых программ является способность комбинировать палитры двух и более изображений и подбирать лучшие цвета для объединенного изображения.

После сокращения палитр отдельных изображений (как это было описано в предыдущем пункте) вы сможете собрать несколько, меньших палитр в одной. Если вы не найдете такую программу, воспользуйтесь редактором, поддерживающим 24-разрядную графику (реальные цвета). Этот тип программ, позволит вам отрезать, и приклеивать различные изображения в одном файле, а затем преобразовать собранное изображение в вашу лучшую 256-цветную палитру;

§          Вам также может потребоваться возможность создания плавных цветовых переходов. Существует множество таких программ и некоторые из них работают с двумя цветами, плавно изменяя окраску от одного оттенка к другому. Иные графические программы позволяют выбрать диапазон цветов в палитре и произвольно смонтировать их. Я предпочитаю последний метод, поскольку он дает наиболее хороший результат и особенно удобен для раскраски битовых образов. Одна из программ, обладающих таким достоинством, называется Electronic Art's Deluxe Paint;

§          Наконец, вы будете очень довольны, если сможете выполнять сглаживание. Это такой технический прием, который позволяет убирать неровности внешнего вида скошенных или закругленных областей путем смешивания промежуточных цветов в шероховатых местах. Если вы используете эту особенность осторожно, то можете сгладить цветовой переход в наиболее контрастных участках и придать изображению более натуральный внешний вид.

Однако существует ряд важных «инструментальных средств», которые невозможно купить ни за какие деньги. Это желание, терпение и хороший художественный вкус. Доведение до совершенства любой задачи требует практики, будь то программирование, кулинария или рисование. Не отчаивайтесь, если ваше первое творение окажется совсем не таким, каким вы его себе представляли. Считайте, что, сделав это, вы уже чему-то научились и двигайтесь вперед.

Теперь давайте рассмотрим основы создания игровой графики.

Уклонение

Пока мы еще не ушли слишком далеко в наших рассуждениях, продолжим нашу Дискуссию разговором о явлении прямо противоположном преследованию — об уклонении. Чтобы сконструировать создание, уклоняющееся от игрока, нам нужно сделать в точности противоположное предыдущим действиям. Алгоритм 13.2 в общих чертах показывает это.

Алгоритм 13.2. Алгоритм Уклонения.

//пусть (рх,ру) - позиция игрока и (ех,еу) - позиция противника

whilе(игра) {

.....// код программы

// Вначале - горизонтальная составляющая перемещения

if ex>px then ex=ex-1

if ex<px then ex=ex+1

//Теперь - вертикальная составляющая

if ey>py then ey=ey-1

if ey<py then ey=ey+1

.... // код программы

В этом месте я еще раз хочу заострить ваше внимание на том, что игры не думают. Персонажи в них только совершают несложные эволюции в пространстве и времени, да определенным образом реагируют на окружающую обстановку и действия игрока. (Некоторые ученые считают, что люди - это не что иное, как набор действий и реакций.)

А теперь перейдем к следующей теме и обсудим такое понятие как «шаблонные мысли».

Улучшения WarEdit

WarEdit уже будет работать вполне удовлетворительно, но на полноценный редактор он все же не тянет. В нем недостает многих деталей, необходимых для настоящей работы. Сейчас я хочу сказать о некоторых моментах, которые вы могли бы доработать сами:

§ Использование разноцветных точек для представления игровых объектов слишком примитивно. Более серьезным и удобным решением было бы использование окна редактирования с возможностью прокрутки, в котором каждый элемент игрового пространства представлен собственной уменьшенной копией;

§ В нашем редакторе любой объект занимает всю ячейку игрового пространства целиком. Но что если мы хотим поместить два мелких предмета в одно и то же место? Здесь могло бы пригодиться окно детализации ячейки;

§ А как быть насчет спецэффектов типа освещения? Неплохо было бы иметь возможность изменять уровни освещения в целом;

§ Еще не помешало бы добавить возможность указания начальных и конечных точек перемещения (телепортации) игрока;

§ Важный технический прием, не примененный в WarEdit, называется полиморфизмом. Эта методика позволяет, используя одну и ту же ссылку, обращаться к различным типам данных. Все структуры данных и определения обычно жестко закодированы в программе и их необходимо импортировать в игру в виде включаемого файла. Но гораздо лучше иметь некоторое подобие синтаксического анализатора, который будет считывать все игровые объекты и значения из файла инициализации.

Можно было бы и дальше продолжить список усовершенствований редактора. Обычно разработчики так и поступают, пока не получат окончательную версию. Фактически, мы могли бы потратить несколько дней и улучшить редактор до уровня Wolfenstein 3-D. (Добавление в него деталей из DOOM отняло бы месяцы). В любом случае, я думаю, у вас уже есть множество идей на этот счет, и если ваш первый редактор окажется вдвое лучше WarEdit'a, то с ним, вероятно, вы создадите и вдвое лучшую игру.

Уменьшение проекционных искажений

Проблема, о которой нам надо поговорить, заключается в проекционном искажении. Как вы знаете, для реализации отсечения лучей мы нарушили правило и использовали одновременно полярные и декартовы системы координат. Это привело к эффекту «рыбьего глаза» (то же самое возникает,когда вы смотрите сквозь сильную линзу).

Это сферическое искажение возникает вследствие использования нами при трассировке лучей радиального метода. Мы рассчитываем все лучи, выходящие из одной точки (позиции игрока). Сферические искажения возникают потому, что все объекты, с которыми пересекаются лучи, определены в «прямоугольном» пространстве. Расчет же лучей проводится в «сферическом» или «полярном» пространстве. Пример такого пространства представлен на рисунке 6.27.

Теперь посмотрим на рисунок 6.28. Мы увидим, что наблюдает игрок, когда смотрит прямо на стену. Он видит прямоугольник. Но так как расстояния до точек пересечения различны, изображение получается искаженным. Рисунок 6.29 показывает два результата отсечения лучей. Первый построен с учетом компенсационных искажений, а второй — без их учета. Все это очень интересно, но как это реализовать? Ответ прост: нужно умножить функцию масштаба на инверсную функцию. Синусоидальное искажение может быть компенсировано умножением масштаба на cos-1

текущего угла по отношению к полю наблюдателя (60 градусов). То есть мы должны умножить каждое значение угла от -30 до +30 на cos-1

того же угла. Это исключит искажение.

Универсальный асинхронный приемопередатчик

ПК оборудованы универсальным асинхронным приемопередатчиком (UART) - чипом, который принимает и передает последовательные данные. Существуют Два наиболее популярных UART для ПК:

Модель 8250;

§ Модель 16550.

Можете считать, что они полностью совместимы друг с другом и нам не нужно выяснять, какой из них используется. Единственным их важным отличием является только то, что модель 16550 имеет внутренний FIFO (First In, First Out - "первый вошел - первый вышел") буфер, который располагает входящие - данные так, что они не могут потеряться вследствие задержки обработки. Теперь взглянем на каждый из регистров UART и на то, как получить к ним доступ. После того как мы обязались написать полную библиотеку для связи, необходимо уяснить, как открыть последовательный порт, а также как осуществлять чтение и запись. Написав однажды,соответствующие функции, мы можем сконцентрироваться на целях игры.

Управление приоритетным состоянием

Можно еще усовершенствовать наш КА, если ввести управление сменой состояний с помощью некоторых переменных и функций. На практике это означает возможность изменения текущего режима, не дожидаясь полного завершения программы, отвечающей за его выполнение.

В имитаторе движения «Мухи» каждое состояние выполнялось до полного завершения. Но если включить в программу проверку выполнения или невыполнения некоторых условий, это позволило бы КА «выпрыгнуть» из состояния, не дожидаясь окончания его «отработки».

Этим заканчивается наш разговор о конечных автоматах, которые могут быть использованы в наших играх для моделирования поведения существ и придания им видимости наличия интеллекта. Теперь к имеющейся у нас системе высокоуровневого управления не помешает добавить низкоуровневое функционирование.

Уравнение плоскости

Я говорил, что мы можем использовать уравнение плоскости для многоугольника, для нахождения значения Z-компонента каждого из пикселей внутри преобразуемого прямоугольника. Вот это уравнение,

Дано: Точка (х,у) и вектор нормали к многоугольнику <Nx,Ny,Nz>

Z = ---------------------------

1- Nx * X – Ny * Y

Ускорение процесса двоичного кодового преооразовзния (бит-блиттинга)

Если подумать о типах разрабатываемых нами компьютерных игр, то станет очевидно, что основной упор нам придется делать на графику.

При работе с такими играми (трехмерные игры, подобные Wolfenstein 3D или DOOM) компьютер большую часть времени тратит на прорисовку стен в трехмерном пространстве или на изображение двухмерных образов спрайтов, представляющих игровые объекты. Мы обсудили изображение в трехмерном пространстве в шестой главе, «Третье измерение». Поэтому теперь я хотел бы остановиться на вопросе оптимизации вывода спрайтов, поскольку это нам особенно понадобится при создании игр данного типа.

В предыдущих главах мы разобрались с понятием бит-блиттинга (глава пятая, «Секреты VGA-карт») и рассмотрели, как передается растровое изображение из одной области памяти в другую. Держу пари, что 90 процентов времени при создании игр уходит на то, чтобы придумать, как ускорить эти процессы. В восемнадцатой главе, «Техника оптимизации», мы обсудим общую теорию оптимизации и разберем несколько примеров использования соответствующей техники после завершения работы над игрой. (Не забывайте о том, что все оптимизационные трюки следует применять на заключительной стадии разработки игры!) Вы должны четко представлять, что для каждой новой игры необходимо заново создавать и реализовывать подходящие алгоритмы битового замещения; более того, вы можете исгюльзовать от двух до пяти различных способов бит-блиттинга в одной и той же игре. При этом каждый из них будет предназначаться для вполне конкретного случая. Например, вы можете обнаружить, что можно оптимизировать функцию бит-блиттинга для объектов, которые на протяжении всей игры остаются неподвижными. Если это так, создайте два преобразования: одно — для движущихся объектов, другое — для стационарных. Код для каждого процесса бит-блиттинга занимает примерно один-два килобайта ияи даже меньше.

Рассмотрим еще один пример возможной оптимизации. Естественно, что чтение данных вашей функцией бит-блиттинга определенным образом зависит от способа их хранения.

И возможно, преобразование будет происходить быстрее, если представить данные в другом виде. Например, вы можете потерять эффективность, сохраняя значения пикселей построчно (в виде двухмерной матрицы), а не по столбцам (по 16 бит). Если иная форма хранения данных дает выигрыш в производительности для некоторых из ваших алгоритмов бит-блиттипга, напишите для них процедуру предварительного преобразования этих данных.

В любом случае, думайте о том, как максимально ускорить процесс бит-блиттинга. Ведь в компьютерной игре на экране присутствуют в среднем от 2 до 20 объектов размером примерно 32х32 пикселя, а это достаточно много для работы в реальном времени.

Примечание

Как вы знаете, я привожу в этой книге некоторые алгоритмы бит-блиттинга. Пожалуйста, не используйте их в ваших компьютерных играх! Они написаны исключительно в демонстрационных целях. Вы должны для каждого конкретного случая найти свой вариант.

Рассмотрим еще один важный аспект бит-блиттинга объектов, который вы сможете с выгодой использовать. Если вы твердо знаете, что размер ваших объектов будет фиксированным (например, 16х16 или 32х32), то можете написать отдельный алгоритм бит-блиттинга, специально оптимизированный для каждого из этих размеров. Помните: не существует общих правил быстрого написания компьютерных игр. Нет уже готовых алгоритмов и написанных кем-то библиотек. Вы должны будете использовать по максимуму весь свой творческий потенциал. Только, не пугайтесь. Даже самая замысловатая игра использует алгебру и геометрию не более чем на уровне высшей школы. Это, конечно, не значит, что вы не можете использовать сверхсложные алгоритмы и забираться в дебри, высшей математики. Однако в результате может оказаться, что двенадцатилетний подросток найдет путь в 100 раз более быстрый и эффективный только потому, что он не такой умный как вы!

Установка обработчика прерывания

Регистрация (или установка) подпрограммы обработки прерываний заключается том, что мы помещаем ее начальный адрес в соответствующее поле таблицы векторов прерываний. Это можно сделать двумя способами:

Мы можем просто изменить адрес прерывания таким образом, чтобы он Указывал на наш собственный обработчик и так все и оставить. Однако при этом, старый обработчик прерывания никогда больше вызываться не будет.

Кроме того, а что произойдет, если прерывание будет сгенерировано именно в тот момент, когда мы будем заниматься заменой адреса в таблице векторов? Р-р-раз и «зависли» — вот что случится! Именно поэтому пусть это действие за вас выполнит DOS при помощи функции _dos_setvect(). Для сохранения старого вектора прерывания следует использовать функцию _dos_getvect(). Обе функции гарантировано изменяют вектора без ущерба для операционной системы;

Очень часто нам требуется расширить функциональные возможности системы без полной замены уже работающих функций. Тогда мы используем цепочку прерываний. Под цепочкой прерывания понимается следующее: мы запоминаем старый адрес процедуры обслуживания прерывания и заменяем его на собственный, затем, по окончании нашей процедуры обработки прерывания, передаем управление старому обработчику. Таким образом, нам удается сохранить чужие обработчики прерываний или резидентные программы - если, конечно, нам это надо!

Взгляните на рисунок 12.3, на котором представлены два способа установки обработчиков прерываний.

Листинг 12.1 демонстрирует установку нашей процедуры обслуживания прерывания timer () (которая по-прежнему ничего не делает).

Листинг 12.1. Установка процедуры обслуживания прерывания.

void (_interrupt _far old_isr) (); // Указатель для сохранения

// вектора старого

// обработчика прерываний

// Сохранить вектор старого обработчика прерывания таймера

old_isr = _dos_getvect( 0х1C);

// Установить новую процедуру обработки прерывания

_dos_setvect(0x1C, Timer);

Ну как, трудно? Да вовсе нет! Для восстановления старого обработчика нам потребуется сделать только:

_dos_setvect(0x1C, old_isr);

Вот и все. Теперь, для примера, заставим наш обработчик прерывания делать что-нибудь полезное, например, обновлять значения глобальной переменной. В Листинге 12.1 показан текст программы SPY.С, которая представляет собой бесконечный цикл, печатающий значение переменной. Единственный способ изменить значение этой переменной - присвоить ей значение из другой программы, например, из обработчика прерывания.

Листинг 12.2. Шпионим за часами (SPY.C)._________________

// ВКЛЮЧАЕМЫЕ ФАЙЛЫ ///////////////////////////////////////////////

#include <dos.h>

#include <bios.h>

#nclude <stdio.h>

#include <math.h>

#include <conio.h>

#include <graph.h>

// ОПРЕДЕЛЕНИЯ//////////////////////////////////

#define TIME_KEEPER_INT 0x1C

// ГЛОБАЛЬНЫЕ

ПЕРЕМЕННЫЕ

///////////////////////////////

void (_interrupt _far *old_Isr)();

// хранит старый обработчик прерывания

long time=0;

// функции ////////////////////////////////////

void _interrupt _far Timer()

{

// Увеличивает глобальную переменную.

// Еще раз отметим, что мы можем это делать, так как при входе

// в процедуру обработки прерывания регистр DS

указывает на сегмент

// глобальных данных нашей программы,

time++;

} // конец Timer

// ОСНОВНАЯ ПРОГРАММА ////////////////////////////////

void main(void)

{

// установка процедуры обработки прерывания

Old_Isr = _dos_getvect(TIME_KEEPER_INT);

_dos_setvect(TIME_KEEPER_INT, Timer) ;

// ожидание нажатия клавиши пользователем

while(!kbhit())

{

// вывод переменной. Примечание: сама по себе функция main

// значение этой переменной не изменяет...

_settextposition(0,0);

printf("\nThe timer reads:%ld ",time);

} // конец while

// восстановление старого обработчика прерывания

_dos_setvect(TIME_KEEPER_INT, Old_Isr) ;

} // конец функции main

Запустив программу, приведенную в Листинге 12.2, вы увидите, что приращение счетчика происходит очень быстро. Фактически, значение этой переменной увеличивается каждую 1/18.2 секунды — так настроены по умолчанию внутренние системные часы. (Не переживайте, очень скоро мы научимся управлять и ими).Главное, что сама программа не увеличивает значенй переменной time. Этим занимается исключительно подпрограмма обслужива ния прерывания.

Итак, мы создали процедуру обслуживания прерывания, установили ее и убедились в том, что она работает - и все это мы сделали, написав лишь несколько строк кода. Восхитительно, не правда ли? Более сложными обработчиками прерываний мы займемся чуть позже. Сейчас же давайте сменим тему и поговорим об игровом цикле.

Установка прерывания

Однажды пройдя через все эти фокусы, чтобы установить простое прерывание, можем окончательно инсталлировать наш собственный вектор ISR, зависящий от СОМ-порта. Запомните, что порты 3 и 4 используют те же самые прерывания, что и порты 1 и 2 соответственно.

Таблица 14.4. Векторы прерывания последовательного порта.

Установка видеорежимов

В играх есть немало технических хитростей: работа со звуком, «искусственный интеллект» и многое другое. Но перед тем как начать этим заниматься, давайте попробуем инициализировать наш дисплей.

Конечно, мы сразу можем набрать гору документации с подробным описанием устройства дисплея, регистров и установок, но все это весьма опасно, и вот почему. То, что будет работать на одной видеокарте, может оказаться абсолютно неработоспособным на другой. Таким образом, чтобы избежать возможной несовместимости, для установки видеорежима мы будем использовать базовую систему ввода/вывода (BIOS).

Можно смело сказать, что основная графическая мощь ПК сосредоточена в прерывании с номером 10h. Использование этого прерывания весьма просто — необходимо правильно установить нужные регистры процессора в зависимости от выполняемой функции. В этой книге мы будем пользоваться режимом 13h (это графический режим с разрешением 320х200 точек, при 256 цветах). Теперь нам нужно найти, как перенести компьютер в этот режим. Для этого давайте напишем программу на ассемблере для установки режима 13h и программу на Си для проверки. Соответствующие фрагменты показаны в Листингах 2.8 и 2.9.

Листинг 2.8. Ассемблерная процедура, устанавливающая видеорежим (SETMODEA.ASM).

.MODEL MEDIUM, С

;модель памяти - MEDIUM, соглашения языка Си

.CODE ;начало кодового сегмента

PUBLIC Set_Mode ;объявляем функцию как общедоступную

Set_Mode PROC FAR С vmode:WORD ;функция получает один параметр

mov АН,0 ;функция 0 прерывания 10h - установка режима

mov AL,BYTE PTR vmode ;номер режима, который вы хотите установить

int 10h ; используем BIOS для установки режима

ret ; возврат из процедуры

Set_Mode ENDP ; конец процедуры

END ;конец кодового сегмента

Листинг 2.9. Си-функция, тестирующая видеорежим (SETMOPEC.C).

#include <stdio.h>

#define VGA256 0х13

#define TEXT_MODE 0х03

extern Set_Mode(int mode);

void main(void)

{

// устанавливаем режим 320х200 точек, 256 цветов

Set_Mode(VGA256);

// ждем нажатия любой клавиши

while (kbhit()) {}

// возвращаем компьютер в текстовый режим

Set_Mode(TEXT_MODE);

} // конец функции main

Теперь если вы наберете и запустите эти программы, то, скорее всего, увидите пустой экран. Правда, в данном случае это не означает «зависание» компьютера, а свидетельствует о том, что VGA-карта переключилась в режим 13h. Стоит только нажать любую клавишу, и вы вновь окажетесь в привычном текстовом режиме 80х25. Конечно, можно было бы использовать функцию _setvideomode() из графической библиотеки Microsoft С, но наша функция работает в сотни раз быстрее.

Теперь, когда мы научились переключать экран в графический режим, неплохо бы попробовать его очистить.

Установки и статус UART

Установки и статус UART управляются через набор внутренних регистров доступных как порты ввода/вывода, адреса которых начинаются от некоторого базового адреса. Базовый адрес определяется номером последовательного порта через который вы хотите связаться. Рассмотрим таблицу 14.1, в которой указаны базовые адреса управляющих регистров UART.

Таблица 14.1. Базовые адреса управляющего регистра UART.

Последовательный порт Базовый адрес порта

СОМ1 3F8h

COM2 2F8h

COM3 3E8h

COM4 2E8h

Как видите, если мы хотим играть через последовательный порт СОМ1, нам необходимо использовать порт 3F8h в качестве базового адреса ввода/вывода. Каждый порт имеет девять регистров, в которые можно писать или из которых можно считывать информацию в зависимости от их типа. Следовательно, для доступа к регистру 1 порта СОМ1 необходимо использовать адрес ввода/вывода 3F8h+1, то есть 3F9n.

Теперь мы знаем, где расположены регистры. А что каждый из них делает?

Это регистр поддержки передачи, куда помещается следующий символ для передачи. Если это одиночный байт и вы используете схему передачи, имеющую менее 8 бит, то данные игнорируются, и не передаются вообще.

Регистр 0 также выполняет функции буферного регистра приема. В зависимости от того, пишете вы в него или читаете из этого регистра, буфер передает или принимает символы с другого компьютера соответственно. В любом случае, при чтении из этого регистра он содержит последний переданный ему символ.

Этот регистр используется, чтобы задействовать тот тип прерываний, который может сгенерировать UART. Он доступен как для чтения, так и для записи. После установки серийного порта было бы неудобно постоянно опрашивать его, поэтому для получения входных данных лучше написать процедуру обслуживания прерывания (ISR), которая будет вызываться каждый раз при получении символа.

Этот регистр позволяет нам сообщить UART'y, какие именно события Должны вызывать прерывание. Для нас представляет интерес только прерывание RxRDY, которое генерируется при получении символа UART'ом.

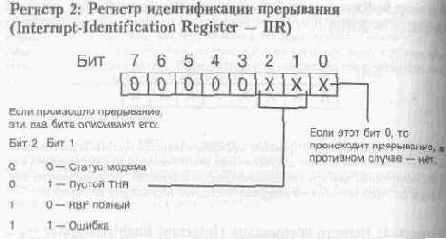
Регистр идентификации прерывания используется для определения причины по которой UART выдал прерывание. Это может показаться избыточным однако если вы предварительно установили UART для получения прерывания по двум или более различным событиям, то, поскольку этот регистр определяет тип произошедшего прерывания, он поможет вам выяснить, что именно произошло.

Регистр управления линией используется для изменения некоторых характеристик последовательного порта, таких как количество передаваемых битов данных, тип четности. Этот регистр также выполняет функции управления загрузкой старшего и младшего байтов делителя, задающего скорость передачи и имеющего WORD. Этот регистр также доступен и для записи, и для чтения.

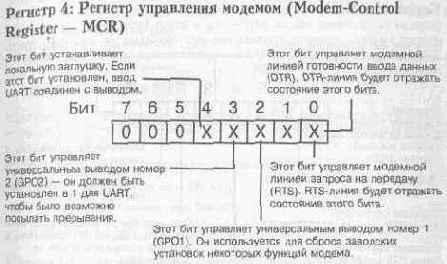
Данный регистр оказывает влияние на некоторые выходные данные линий управления модема. Нас больше всего в нем интересует бит GP02. Когда он установлен, появляется возможность прихода прерываний.

Регистр состояния линии используется, чтобы обрисовать состояние коммуникационного порта. В этом регистре нас интересует пятый бит (ТВЕ), который используется для определения возможности продолжения передачи символов (THR).

Регистр состояния модема используется, чтобы показать состояние линий управления модемом. Для наших целей этот регистр едва ли понадобится. Однако вы могли бы найти применение индикатору звонка (RI). Вы можете написать программу, которая будет перехватывать звонок и когда вызывается ваш номер, например, сообщать об этом соответствующей надписью на экране и звуком.

Регистр 7: Регистр временного заполнения (Scratch-Pad Register)

Не используется

Регистр 8: Менее значимый ключ делителя скорости передачи (Baud-Rate Divisor Latch Least-Significant Byte - DLL)

Предназначен для хранения младшего байта делителя, используемого при вычислении действительной скорости передачи через порт.Окончательная скорость вычисляется так: берут младший и старший банты и используют их как делитель числа 115200. В результате получится скорость передачи. Этот регистр доступен через регистр 0 при установленном 7-м бите (DLAB) регистра З (LCR).

Регистр 9: Регистр более значимого байта ключа делителя скорости пepeдaчи,(Baud-Rate Divisor Latch Most-Significant Byte-DLM)

Этот регистр используется для поддержки старшего байта делителя, использумого для вычисления действительной скорости передачи через последовательный порт. Окончательная скорость передачи вычисляется следующим образом: берут старший и младший байты и используют их как делитель, на который нужно разделить число 115200. Это дает скорость передачи. Данный регистр доступен через регистр 1 при установленном 7-м бите (DLAB) регистра 3 (LCR).

Устранение эффекта сдвига кадра

На медленных машинах или на машинах с медленными видеокартами можно заметить некий сдвиг изображения, как будто оно копируется на экран. Из-за эффекта сдвига изображение выглядит как бы разорванным. Этот интересный но нежелательный эффект появляется оттого, что адаптер сканирует видеобуфер и рисует изображение на дисплее примерно 60 раз в секунду. Этот процесс называется регенерацией экрана. Если программа в момент начала регенерации дисплея находится в процессе рисования кадра, вы заметите эффект сдвига изображения.

К счастью, существуют методы проверки статуса регенерации экрана. На VGA-карте есть регистр, сообщающий, регенерируется ли экран в настоящее время- Все, что требуется для устранения эффекта сдвига кадра, это подождать, пока регенерация экрана завершится. Затем можно начать рисовать изображение.

В Листинге 17.7 содержится фрагмент программы, ожидающей завершения цикла регенерации экрана. Это дает вам примерно 1/60 секунды, чтобы нарисовать следующий кадр. Данный фрагмент можно поместить непосредственно перед функцией, перемещающей кадр из системной памяти в видеобуфер. Выполняйте такую проверку каждый раз перед копированием буфера на экран. Только на очень быстрых машинах или при использовании небольшого окна вывода, одной шестидесятой секунды будет достаточно для изображения нескольких планов и их копирования на экран. Это главный недостаток режима 13h. Единственная альтернатива проверке на регенерацию экрана — это использование видеорежимов, поддерживающих несколько видеостраниц, и переключение между ними.

Листинг 17.7. Проверка вертикальной трассировки.

asm mov dx,0x3da

NoRetrace:

asm in al,dx

asm and al,8

аsm jz NoRetrace // ждать, пока трассировка завершится

Retrace:

asm in al,dx

asm and al,8

asm jnz Retrace // ждать начала трассировки

Программа в этой главе не выполняет проверку вертикальной трассировки. Это было сделано для того, чтобы свести к минимуму использование ассемблера. Настоятельно рекомендую использовать этот фрагмент во всех программах вывода графики.

Устройство и архитектура звуковой карты Sound Blaster

Sound Blaster — сложная звуковая карта с большими возможностями. Управлять ею не так уж и просто, и мы наверняка не сможем рассмотреть все ее впечатляющие способности в одном-единственном разделе. Поэтому мы приведем здесь только основные характеристики современных моделей Sound Blaster и кратко остановимся на их функциональных различиях.

На данный момент существует четыре различных модификации Sound Blaster. Их характеристики приведены в таблице 9.1.

Sound Blaster может создавать два типа звуков:

§ Синтезированный звук;

§ Оцифрованный звук.

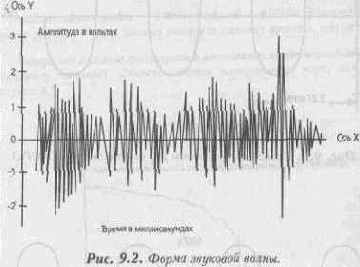
Синтезированный звук создается искусственно с помощью электронной аналоговой или цифровой аппаратуры. В Sound Blaster применяется современный подход к синтезу звука — метод цифровой частотной модуляции (FM synthesis). В этом методе для создания звука используется та самая частотная модуляция, которую используют и музыкальные радиостанции, работающие в УКВ-диапазоне. Мы поговорим об этом подробнее позже в этой главе.

Sound Blaster также имеет процессор цифровых сигналов (digital signal processor, DSP), который помогает в синтезе и воспроизведении MIDI-музыки. По-существу, MIDI (musical instrument digital interface, цифровой интерфейс электромузыкальных инструментов) — это стандарт для оцифровки голоса и инструментальной музыки таким образом, чтобы они могли быть воспроизведены с помощью компьютера или такого синтезатора, как Yamaha.

Кроме синтеза звука Sound Blaster позволяет оцифровывать; а затем воспроизводить такие звуковые фрагменты, как речь или различные эффекты. Это очень полезное свойство, так как некоторые звуки очень сложно или даже невозможно создать только с помощью частотного синтезатора и DSP. В наших играх мы как раз и будем использовать оцифрованные звуковые эффекты вместе с MIDI-музыкой.

В следующем разделе мы рассмотрим как Sound Blaster работает с оцифрованным звуком.

В каком формате должны быть представлены данные MIDI?

В случае настоящего MIDI-устройства, такого как MPU401 или SoundCanvas, ему будут передаваться данные MIDI без каких-либо изменений (исключая сообщения SysEx).

В случае Adiib или Sound Blaster, MIDPAK будет эмулировать устройство MIDI и эта эмуляция имеет определенные ограничения;

Каналы 2-9 используются для мелодических инструментов;

§ Канал 10 используется для ударных инструментов;

§ Загружаемые алгоритмы должны быть в формате обобщенного MIDI.

Вектор Номер Адресная функция

0х0В 0x002C-0x002F RS-232 порт 1

0х0С 0х0030-0х0033 RS-232 порт 2

Все что нам нужно сделать для установки нового ISR, это использовать функцию Си _dos_getvect(), чтобы запомнить прежнее значение вектора, и _dos_setvect(), чтобы инсталлировать наш собственный ISR на место старого. Далее, с приходом прерывания (то есть когда получен символ), будет вызываться наша процедура. Звучит это великолепно, но что она будет делать?

Наш ISR должен выполнять только одну задачу — получить символ из регистра приемного буфера (RBR) и поместить его в программный буфер. Чтобы основная программа могла брать поступающие символы по мере надобности, мы должны буферизировать ввод. С этой мыслью создадим буфер с перезаписью и установим его размер равным 128 байтам, хотя, вообще-то, его длина может быть любой.

Алгоритм буферизации работает так. Полученный из RBR следующие символ помещается в буфер в текущую позицию. Далее текущий индекс буфера инкрементируется. Когда позиция записи в буфере доходит до конца, она перемещается к началу. Как вы понимаете, при этом данные, которые были записаны ранее, окажутся перекрыты. Надеюсь, что до того, как это произойдет основная программа успеет прочитать символы из буфера и обработать полученные данные. Рисунок 14.3 поясняет принцип работы буфера с перезаписью.

Мы должны обсудить еще одну тонкость, прежде чем закончим разговор об ISR. Непосредственно перед выходом из процедуры обработки прерывания необходимо сообщить PIC'y о ее завершении. Для этого в конец процедуры нужно вставить команду записи в порт 20h значения 20h. Если этого не сделать, произойдет сбой системы. Но это — между прочим, ибо пока вы используете функции Си, об этом не стоит беспокоиться. Вот если бы вы решили писать программы исключительно на ассемблере, то вопрос правильного завершения прерываний оказался бы весьма актуален и мы обсудили бы его более подробно. Но давайте пока остановимся на Си.

Листинг 14.1 показывает операции с ISR.

Листинг 14.1. Операция ISR.

void _interrupt _far Serial_Isr(void)

{

// Это процедура обработки прерывания СОМ-порта. Она очень проста.

// При вызове она читает полученный символ из регистра 0 порта

//и помещает его в буфер программы. Примечание: язык Си сам

// заботится о сохранении регистров и восстановлении состояния

// запрещаем работу всех других функций

//во избежание изменения буфера

serial_lock = 1;

// записываем символ в следующую позицию буфера

ser_ch = _inp(open_port + SER_RBF);

// устанавливаем новую текущую позицию буфера

if (++ser_end > SERIAL_BUFF_SIZE-1) ser_end = 0;

// помещаем символ в буфер

ser_buffer[ser_end] = ser_ch;

++char_ready;

/ / восстанавливаем состояние контроллера прерываний

_outp(PIC_ICR,0x20);

// разрешаем работу с буфером

serial_lock = 0;

} // конец функции

Программа из Листинга 14.1 выполняет все то, о чем мы говорили. Однако стоит обратить внимание на одну маленькую деталь. В программу включена переменная serial_lock, которая оберегает основную программу от конфликт тов связанных с обращением к буферу, пока ISR обновляет его. Такой прием называется «блокировкой» или «семафором». В DOS'e подобной проблемы никогда не возникает по ряду причин, о которых говорить слишком долго. Необходимость регулирования доступа к общим данным возникает только для полностью многозадачных систем. Тем не менее, введение «семафоров» - хорошая практика, даже если на данном этапе такая техника и не нужна. Все, мы почти у цели!

Вероятностные автоматы

Наверное, вы уже поняли, как вероятность и случайные числа могут быть использованы для выбора направлений и состояний. Мы научились использовать случайные последовательности для конструирования «характера» персонажей. Я имею в виду, что «Муха» в нашем предыдущем примере могла самостоятельно выбирать различные состояния, основываясь на окружающей обстановке. Если несколько изменить метод выбора состояний, основанны на генерации случайных чисел (то есть, создать условия, при которых вход в опредёленное состояние стал бы легче или тяжелее), то, в конечном счете, нам удалось бы изменить "характер" «Мухи».

Скажем, нам захотелось иметь в игре две «мухи». Если одну и ту же программу использовать для создания траектории движения каждой «мухи», они бы действовали одинаково. Во многих случаях большего и не требуется. Однако гораздо интересней иметь много «мух» с небольшими различиями в поведении. Это можно было бы реализовать изменением диапазона случайных чисел-во всех строках программы, где выбираются состояния «мухи». Но такой подход будет очень грубым. Мы пойдем другим путем — путем создания общего метода управления характером персонажей, основанного на вероятности.

В искусственном интеллекте «индивидуальность» означает возможность существ по-разному выполнять определенные действия при одних и тех же обстоятельствах. Например, у меня есть несколько достаточно активных друзей, которые захотели бы слегка проучить плута, попытавшегося их надуть. Но у меня также есть друзья, которые более спокойны и предпочитают сначала думать, а потом действовать. Скорее всего, мошеннику удалось бы как-то с ними договориться. То, что мы видим на данном примере и является «индивидуальностью». Каким именно способом это будет достигнуто, не принципиально, важен конечный результат.

В видеоиграх мы могли бы иметь несколько противников, которые постоянно преследуют нас, пока другие в это время неподвижны и стреляют. Третьи трусливы и предпочитают убегать, а не сражаться. Анализируя ситуацию, мы видим, что имеется все тот же набор состояний, но вероятности перехода в них различны для каждого создания.

Попытаемся вначале проанализировать проблему. Нам необходимо определить вид объекта, который зависит от направления взгляда игрока и траектории объекта или направления его движения. Как мы уже говорили, луч зрения игрока можно зафиксировать и считать, что он всегда перпендикулярен экрану. Тогда нам нужно будет побеспокоиться только о векторе траектории объекта, выводимого на экран. На рисунке 8.7 изображена взаимосвязь между вектором направления взгляда игрока и некоторой траекторией передвижения объекта.

Вертикальный обратный ход луча

Образ, рисуемый на экране ЭЛТ (электронно-лучевой трубки) и управляемый картой VGA, образуется в результате взаимодействия следующих факторов:

§ Луч электронов движется, по экрану слева направо и сверху вниз, рисуя картинку;

§ Когда он достигает нижней границы, он вновь возвращается вверх и все начинается сначала.

Рисунок 5.16 показывает это.

§ Чтобы вернуться в исходную позицию, лучу требуется примерно 1/60 секунды. Это идеальное время для обновления видеобуфера. В течение этого периода видеобуфер недоступен VGA-карте. Таким образом, 1/60 секунды — это аппаратно-зависимый параметр.

В седьмой главе, «Продвинутая битовая графика и специальные эффекты», мы узнаем, как «синхронизировать» наши игры с этим сигналом и создать чистые, свободные от мерцания изображения.

Video for Windows

Когда все ваши технические проблемы решены и вы получили приличное видеоизображение вашего макета, настало время использовать компьютера программное обеспечение (или, скорее, я бы сказал, его отсутствие) для того, чтобы перевести его в цифровую последовательность. Я сам не люблю понапрасну тратить много денег, и поэтому не буду и вас убеждать приобрести оборудование и программное обеспечение на сотни или тысячи долларов. Следовательно, нам придется использовать то, что поставляется с платой ввода графической информации. Я имею в виду Microsoft Video for Windows, которая, в общем-то, предназначена, скорее, для оцифровки сюжетов, а не для моментальных снимков вроде наших.

Так как почти все платы ввода графической информации продаются вместе с Microsoft Video for Windows, я хочу рассказать, как использовать Video for Windows для обработки образов ваших игровых объектов.

При создании каждого кадра используйте опцию single-frame (одиночный кадр);

§ Создав кадр, сохраняйте его в формате BMP-файла, а затем с помощью другой программы преобразуйте его в PCX-формат.

§ При создании кадров с вращающимся объектом расположите под ним круглый транспортир, чтобы точно повернуть объект на нужное количество градусов. Затем, когда вы оцифруете все ваши образы, запишите их в файлы с именами nameххх.bmp, где ххх - угол поворота. Я считаю, что для получения вполне реалистичной картины движения, перед очередным кадром можно поворачивать объект на 30°.

§ Завершив оцифровку всех кадров, вы должны преобразовать их в формат PCX с помощью какого-нибудь графического редактора или специализированной программы. (Большинство графических редакторов для персональных компьютеров поддерживают PCX-файлы в режиме 320х200х256.)

§ После того как все ваши файлы сохранены в формате PCX, нужно тщательно вычистить из них фон и попавшую в кадр платформу.

§ Затем возьмите все кадры и разместите их в одном файле PCX с общей палитрой. Я пришел к выводу, что для получения реалистичного изображения не требуется изготавливать картинки размерами более чем 128х128 пикселей.

Описанная здесь последовательность действий в виде алгоритма представлена на рисунке 8.13.

ВИДЕОИГРЫ. ПЕРВЫЕ ШАГИ...

С чего начать? Хочется так много сказать, что невольно придется посвятить этому несколько страниц. То путешествие, которое мы собираемся предпринять в мир разработки видеоигр, можно смело назвать захватывающим приключением. Создание видеоигр можно сравнить с написанием стихов или рисованием картины. Для этого нужно вдохновение, ведь создатель хочет поделиться с окружающим миром частичкой своего воображения. Один великий скульптор сказал однажды; «Статуя была здесь всегда, Я просто освободил ее из камня». Это высказывание вполне применимо и к видеоиграм.

Компыотер — это просто хранилище битов информации и, устанавливая их в 1 или 0, вы создаете образ. В этом заключается искусство. Я хочу, чтобы вы настроились на созидательную работу. Нам потребуется полное взаимопонимание. В этой главе я расскажу о том, как создаются видеоигры. Вы узнаете вот о чем:

Кто пишет видеоигры;

§ Откуда берутся идеи;

§ Фазы создания видеоигры;

§ Что вы узнаете из этой книги.

В следующих главах вы узнаете, как писать игры.

Видимый объем

Как мы узнали в главах, посвященных трехмерной графике, базирующейся на многоугольниках (глава шестая, «Третье измерение» и седьмая, «Улучшенная битовая графика и специальные эффекты»), объекты должны быть отсечены в пределах видимого объема (или усеченной пирамиды просмотра). Это достигается путем определения ребер каждого многоугольника и отсечения их шестью гранями видимого объема. Возникающая при этом проблема состоит в том, что объем просмотра представляет собой трехмерный трапецоид, состоящий из шести интересующих нас плоскостей, так как это показано на рисунке 8.3.

Мы, конечно, не хотим рассчитывать пересечения спрайтов с произвольными плоскостями. Это было бы уж слишком! Но если мы вначале спроецируем каждый спрайт в аксонометрии и рассчитаем их масштаб, то сможем превратить объем просмотра в прямоугольник. Теперь, так как мы выполняем обратную операцию, мы сможем отсечь спрайты куда как более легким образом, чем при использовании уравнений произвольных плоскостей.

Этот прием основывается на том факте, что объем просмотра уже является аксонометрической проекцией. Если мы отсечем края трехмерного объекта? видимым объемом прежде, чем спроецируем этот объект, мы будем обязаны использовать трапецеидальные формы объема просмотра. Однако, если мы вначале спроецируем объект с учетом перспективы, а затем

отсечем его прямоугольными границами видимого объема, то.результат, полученный таким образом, будет полностью совпадать с результатом, достигаемым первым способом. Отсечение же в плоскостях, параллельных плоскости просмотра, сводится к простому условному оператору, в котором проверяется, является ли спрайт слишком далеким или слишком близким по отношению к вам.

В случае видеорежима l3h мы можем отсекать все спрайты по размерам экрана или четырехугольника, границы которого определяют точки (0,0) и (319,199). Отсечение в плоскостях, параллельных плоскости просмотра, осуществляется с помощью простого теста на выполнение условия: если спрайт находится внутри наблюдаемого Z-пространства, то визуализируйте объект, а в противном случае игнорируйте его. Отсечение в этих плоскостях выглядит так просто оттого, что в действительности спрайты — это прямоугольные многогранники, расположенные перпендикулярно линии взгляда, или параллельно плоскости просмотра (вы можете думать, как вам больше нравится, но на самом деле это одно и то же).

Я полагаю, что, поэкспериментировав с отсечением дальней плоскостью, вы сделаете так, чтобы объект размером меньше, чем в один пиксель по любому измерению (после масштабирования) вообще не рисовался. Выбирая ближнюю плоскость отсечения, старайтесь сделать так, чтобы приближающийся объект не выглядел как под микроскопом с многократно увеличенными пикселями.

Вопросы и ответы

В этом разделе приведены ответы на наиболее часто задаваемые вопросы, касающиеся озвучивания игр.

При исполнении MIDI-музыки с помощью пакета программ MIDPAK мне кажется, что часть музыкальной композиции теряется

Проверьте назначение каналов. Эмуляция MIDI на Sound Blaster и других картах происходит на каналах 2-9 для мелодических инструментов и на 10 канале для ударных. Многие программы записывают последовательности MIDI, начиная с канала 1. При эмуляции MIDI пакетом MIDPAK канал 1 игнорируется. Назначения каналов MIDPAK были разработаны для эмуляции Roland МТ-32. Несмотря на ряд усовершенствований для поддержки обобщенного MIDI, каналы все еще ограничены номерами со второго по девятый и десятым.

При исполнении MIDI-музыки с помощью пакета программ MIDPAK, она звучит иначе, чем при использовании моего собственного музыкального контроллера. Почему?

Ваш контроллер использует другие алгоритмы, нежели MIDPAK. Чтобы избежать этого, необходимо обратиться к профессиональному композитору, который сможет скорректировать вашу композицию для исполнения с помощью MIDPAK. Однако эти услуги вряд ли будут бесплатными.

Мне не удается изменить громкость с помощью MIDPAK. Почему?

Уровень громкости в MIDPAK изменяется относительно базового уровня данного канала. MIDPAK не может изменить громкость, если вы не определили базовый уровень для каждого канала в вашем файле MIDI. Вы можете определить базовую громкость для MIDI-канала, используя Контроллер 7.

Могу ли я использовать один и тот же MIDI-файл для всех звуковых карт?

Нет, но вы можете сделать нечто похожее. Во-первых, сделайте запись в стандарте обобщенного MIDI. Затем ее нужно скорректировать для Sound Canvas, MIDI, OPL2/OPL3 и МТ-32. Базовые уровни громкости и качество звучания разных алгоритмов для этих устройств немного различаются. Исходные тексты программы SETM (программа конфигурации MIDPAK) входят в поставку (файл SETUP.ZIP) и, в зависимости от звукового драйвера выбранного пользователем, вы можете копировать различные версии вашей музыки.

Восприятие игры

Человеку, который собрался поиграть в компьютерную игру, хочется чтобы она была интерактивной. В данном случае под словом интерактивная я подразу меваю то, что графическое изображение должно быть четким и быстро сменяться. При этом музыка должна звучать в соответствующем темпе и игра обязана мгновенно реагировать на действия игрока (по крайней мере, с точки зрения играющего). Игроку должно казаться, что все (музыка, графика, звуковые эффекты и т. д.) происходит одновременно. Теперь взглянем на это с точки зрения программиста.

Вообще-то, сделать так, чтобы разные события в игре происходили одновременно, сложно. Персональный компьютер — это не многозадачная система (во всяком случае, не для игр, работающих под управлением DOS). Более того, у персонального компьютера только один процессор. Следовательно, иллюзия реальности или "реального времени" должна создаваться как-то иначе. Этот иной способ опирается исключительно на скорость работы компьютера. Быстродействие компьютера настолько превышает скорость человеческого восприятия, что машина успевает выполнять все операции последовательно, а человеку кажется, что все происходит одновременно.

На самом деле, в компьютерной игре все происходит примерно следующим образом: мы получаем команды пользователя, реагируем на них в соответствии с логикой игры, выводим на экран изображения объектов и озвучиваем происходящие события, затем повторяем все снова и снова. Благодаря тому, что это происходит десятки, если не сотни, раз в секунду, нам удается заставить игрока поверить в существование созданного нами виртуального мира.

Воспроизведение оцифрованного звука

Теперь поговорим о воспроизведении оцифрованных звуков. Я не буду показывать вам, как оцифровывать звуки. Вы сами можете воспользоваться одним из десятков программных пакетов, предназначенных для этой цели. Тем более, что в самой компьютерной игре звук не надо записывать, его надо воспроизводить!

Из этих соображений я снабдил эту главу условно-бесплатной программой Blaster Master. Эта программа работает в среде MS-DOS и позволяет делать с оцифрованным звуком все что угодно. Она может записывать звук в файлы различных форматов и применять к звуку специальные эффекты (эхо, реверберацию, смену тональности и т. д.)

Примечание

Оцифрованный звук, как и любая другая информация, должен иметь определенный формат для хранения данных. На персональных компьютерах наиболее распространены форматы WAV и VOC. Оба из них, кроме собственно звуковых данных, имеют специальные заголовки. Формат WAV был предложен в Windows, а формат VOC является стандартом «де-факто».

Blaster Master способен преобразовывать данные из формата VOC в формат WAV и обратно. Демонстрационные игры, которые мы будем рассматривать в этой книге, используют исключительно формат VOC. Поэтому, прежде чем использовать свои звуковые эффекты с нашими примерами программ, вы должны записать их как VOC-файлы или преобразовать их в этот формат, иначе ничего не выйдет! Мы выбрали этот формат из-за того, что он проще для понимания. Кроме того, WAV-файлы могут быть записаны только с частотой 11,22 или 44КГц, а это приводит к большому расходу памяти.

С чего мы начнем? Неплохой вопрос. Начнем-ка мы с драйвера. Чтобы проигрывать звуки, нам понадобится драйвер CT-VOICE.DRV, поставляемый фирмой Creative Labs. Этот драйвер позволяет нам вызывать функции работы со звуковой картой, точно так же, как мы вызываем системные функции BIOS.

Однако этот драйвер не является расширением BIOS и этим отличается от драйверов джойстика и мыши. Он использует другую технологию, называемую загружаемыми драйверами устройств. При таком подходе, драйвер загружается в память и реализованные в нем функции исполняются посредством передачи управления по определенному смещению относительно начала кода драйвера.

Передача параметров функциям драйвера осуществляется загрузкой их значений в определенные регистры процессора.

(Впервые я столкнулся с этой технологией около семи лет назад. И хотя я уже долгое время занимался программированием, не сразу сообразил, что мне надо самостоятельно загрузить драйвер в память, а затем передать ему управление.)

CT-VOICE.DRV имеет множество команд, и я не буду детально обсуждать каждую из них. Поговорим только о тех, которые потребуются нам для загрузки и воспроизведения оцифрованных звуков. В таблице 9.2 приведены необходи мые нам функции драйвера.

Таблица 9.2. Подмножество функций драйвера CT-VOICE.DRV.

Функция

Возвращение параметров в вызывающую функции

Когда Си только начинал создаваться, одним из требований в спецификациях называлась «функциональность» языка. Под функциональностью я понимаю возвращение результата и возможность использования комплексных выражений. Например, рассмотрим следующее выражение на Си:

coeff = Factorial(n)*cos(r)*Scale(z);

Это выражение использует три функции и выполняет требуемые математические операции. Результат сохраняется в переменной coeff. Именно это и делает Си «функциональным» языком.

Конечно, это только одна из многих возможностей Си. Таким образом, если мы хотим эмулировать с помощью ассемблера настоящие Си-функции, мы должны иметь возможность возвратить результат в вызывающую функцию, как это делает Си.

Если вы скомпилируете парочку Си-функций, возвращающих значение, и посмотрите на их ассемблерные листинги, то вскоре заметите, что функции всегда возвращают результат в строго определенном наборе регистров. Если же вы прислушаетесь к моим советам, то я гарантирую, что ваши ассемблерные функции будут, по крайней мере, правильно возвращать результаты.

В зависимости от типа, возвращаемые в Си параметры должны находиться в следующих регистрах:

BYTE

возвращается в регистре AL;

§ WORD

возвращается в регистре АХ;

§ DWORD должно возвращаться ,в, паре DX:AX, причем в АХ записывается

§ младшее слово;

§ Указатели типа NEAR должны возвращаться в регистре АХ;

§ Указатели типа FAR Возвращаются в паре DX:AX, причем в DX должен содержаться сегмент, а в АХ - смещение.

Давайте для примера вспомним Листинг 2.2, где мы складывали два целых числа и накапливали результат в АХ. К счастью, это именно тот регистр, в котором целое значение может быть возвращено в Си-программу. Если же встречается другая ситуация, (например, результат находится в регистре СХ). то для корректной передачи результата мы должны перед выходом переместить полученное значение в АХ.

Так... Вроде бы, с директивами и техникой программирования на ассемблере MASM мы покончили. Теперь я предлагаю перейти к более живым примерам. Кстати, для них-то все это и написано.

Вращение объектов

Для того чтобы вращать объект, мы должны повернуть его вокруг одной из координат. В двухмерной графике для этого обычно выбирается ось Z. Пока мы находимся в двухмерном мире, нас не беспокоит третье измерение - мы просто не придаем ему значения.

Если экран — это плоскость X-Y, то ось Z — это перпендикуляр к осям Х и Y. Таким образом, если мы описываем наши объекты относительно двухмерного мира, то у нас появляется возможность вращать их относительно оси Z,

Следующие формулы позволяют вращать произвольную точку (X,Y) относительно оси Z:

new_x = x*cos(angle) - y*sin(angle) new_у = y*cos(angle) + y*sin(angle)

где angle — это угол, на который вы хотите повернуть точку. Кроме этого вам стоит помнить еще пару вещей:

§ Положительные углы имеют эффект вращения по часовой стрелке;

§ Отрицательные углы имеют эффект вращения против часовой стрелки.

Надо также не забывать, что Си использует для своих функций радианы, а не градусы, и все вызовы тригонометрических функций должны передавать в параметрах также радианы. Для того чтобы перевести радианы в градусы, мы должны написать простые макросы.

Deg_To_Rad(deg) {pi*deg/180;}

Rad_To_Deg(rad) {180*rad/pi;}

Другими словами, это значит, что в круге 360 градусов или 2хPi радиан. Теперь нам нужно написать функцию для вращения объекта. Давайте просто используем формулы, не задумываясь о том, как и почему они работают. Функция в Листинге 4.7 делает именно то, что мы хотим.

Листинг 4.7. Вращение объекта.

void Rotate_0bject(object__ptr object, float angle)

{

int index;

float x_new, y_new,cs, sn;

// сначала вычислим синус и косинус угла

сs = cos(angle) ;

sn = sin(angle);

// поворачиваем каждую вершину на угол angle

for (index=0; index<object->num_vertices; index++)

{

x_new = object->vertices [index].x*cs-object->vertices[index].y*sn;

y_new = object->vertices [index].y*cs+object->vertices[index].x*sn;

// изменяем исходные координаты.на расчетные

object->vertices[index].x = x_new;

object->vertices[index].y = у_new;

} // конец цикла for

} // конец функции

Думаю, что надо кое-что объяснить. Я вычисляю заранее значения синуса и косинуса для данного угла. Зачем, спросите вы. Ответ прост — для скорости. Ибо заниматься вычислениями тригонометрических функций в процессе работы программы можно позволить себе только, имея математический сопроцессор.

Теперь настало время написать что-нибудь посерьезней. Мне кажется, что надо бы написать что-то более экстравагантное, чем одинокий астероид. Пусть это будут хотя бы несколько астероидов. Давайте сначала спланируем наши дальнейшие действия.

Я хотел бы иметь поле астероидов различных размеров в количестве более 100 штук. И так, чтобы они могли вращаться. Для этого программа должна иметь следующую структуру:

Шаг 1. - Инициировать поле астероидов;

Шаг 2. - Стереть поле астероидов;

Шаг 3. - Трансформировать поле астероидов;

Шаг 4. - Нарисовать поле астероидов;

Шаг 5. - Перейти к Шагу 2, пока пользователь не нажмет на кнопку.

Чтобы сделать это проще, я добавил три новых поля к нашей структуре: одно для угла поворота и два - для скорости (целиком программа представлена в Листинге 4.8).

Листинг 4.8. Программа, которая рисует поле астероидов (FIELD.С).

// ВКЛЮЧАЕМЫЕ ФАЙЛЫ ////////////////////////////////////

#include <stdio.h>

#include <graph.h>

#include <math.h>

// ОПРЕДЕЛЕНИЯ /////////////////////////////////////////

#define NUM_ASTEROIDS 10

#define ERASE 0

#define draw 1

// СТРУКТУРЫ ДАННЫХ ////////////////////////////////////

//определяем структуру "вершина"

typedef struct vertex_typ

{

float x,y; // координаты точки на плоскости

} vertex, *vertex__ptr;

// структура объекта

typedef struct object_typ

{

int num_vertices;     // количество вершин объекта

int color;            // цвет объекта

float xo,yo;          // позиция объекта

float x_velocity;     // скорость перемещения по осям Х

float y_velocity;     // и y

float scale;          // коэффициент масштабирования

float angle;          // угол поворота

vertex vertices[16]; // 16 вершин

}object, *object_ptr;

// Глобальные переменные //////////////////////////////

object asteroids[NUM_ASTEROIDS];

// Функции ////////////////////////////////////////////

void Delay(int t)

{

// функция формирует некоторую временную задержку

float x = 1;

while(t—>0)

x=cos(x);

} // конец функции /////////////////////////////////////

void Scale_Object(object_ptr object,float scale)

{

int index;

// для всех вершин масштабируем координаты х и у

for (index = 0; index<object->num_vertices; index++)

{

object->vertices[index].x *= scale;

object->vertices[index].y *= scale;

}// end for index

// конец

функции ///////////////////////////////////////////

void Rotate_Object(object_ptr object, float angle)

{

int index;

float x_new, y_new,cs,sn;

// заранее вычислить синус и косинус

cs = cos(angle);

sn = sin(angle);

// поворачиваем каждую вершину на угол angle

for (index=0; index<object->num_vertices; index++)

{

x new = object->vertices[index].x * cs - object->vertices[index].y * sn;

у new = object->vertices[index].y * cs + object->vertices[index].x * sn;

object->vertices[index].x = x_new;

object->vertices[index].y = y_new;

} // конец цикла for

} // конец функции //////////////////////////////////////////////////

void Create_Field(void)

{

int index;

// формируем поле астероидов

for (index=0; index<NUM_ASTEROIDS; index++)

{

// заполнить

все поля

asteroids[index].num_vertices = 6;

asteroids[index].color = 1 + rand() % 14; // всегда

видимый

asteroids[index].xo    = 41 + rand() % 599;

asteroids[index].yo    = 41 + rand() % 439;

asteroids[index].x_velocity = -10 + rand() % 20;

asteroids[index].y_velocity = -10 + randO % 20;

asteroids[index].scale = (float)(rand() % 30) / 10;

asteroids[index].angle = (float) (-50+(float)(rand()%100))/100;

asteroids[index].vertices [0].x =4.0;

asteroids[index].vertices[0].у = 3.5;

asteroids[index].vertices[l].x=8.5;

asteroids[index].vertices[1].y = -3.0;

asteroids[index].vertices[2].x = 6;

asteroids[index].vertices[2].у = -5;

asteroids[index].vertices[3].x = 2;

asteroids[index].vertices[3].у =—3;

asteroids[index].vertices[4].x = -4;

asteroids[index].vertices[4].у = -6;

asteroids[index].vertices[5].x = -3.5;

asteroids[index].vertices[5].у =5.5;

// теперь масштабируем каждый астероид до нужного размера

Scale_Object((object_ptr)&asteroids [index],

asteroids[index].scale) ;

} // конец цикла for

} // конец функции ///////////////////////////////////////////////////////

void Draw_Asteroids(int erase)

{

int index,vertex;

float xo,yo;

for (index=0; index<NUM_ASTEROIDS; index++)

{

// рисуем астероид

if (erase==ERASE)

_setcolor(0);

else

_setcolor(asteroids[index].color);

// получить позицию объекта

xo = asteroids[index].xo;

yo = asteroids[index].yo;

// перемещаемся к первой вершине

_moveto((int)(xo+asteroids[index].vertices[0].x),

(int)(yo+asteroids[index],vertices[0].y));

for (vertex=1; vertex<asteroids[index].num_vertices; vertex++)

{

_lineto((int)(xo+asteroids[index].vertlces[vertex].x),(int) (yo+asteroids[index].vertices [vertex].y));

} // конец цикла for

по вершинам

// замыкаем

контур

_lineto((int)(xo+asteroids[index].vertices[0].x), (int)(yo+asteroids[index].vertices[0].y));

} // конец цикла for

по астероидам

} // конец

функции                                      ///////////////////////////////////////////////////////////////////////////////////////////

void Translate_Asteroids()

{

int index;

for (index=0; index<NUM_ASTEROIDS; index++) {

// перемещаем

текущий астероид

asteroids[index].xo += asteroids[index].x_velocity;

asteroids[index].yo += asteroids[index].y_velocity;

if (asteroids[index].xo > 600 || asteroids[index].xo < 40)

{

asteroids[index].x_velocity = -asteroids[index].x_velocity;

asteroids[index].xo += asteroids[index].x_velocity;

}

if (asteroids[index].yo > 440 || asteroids[index].yo < 40)

{

asteroids [index].y_velocity = -asteroids[index] .y_velocity;

asteroids[index].yo += asteroids[index].y_velocity;

}

} // конец цикла for

} // конец функции

///////////////////////////////////////////////////////

void Rotate_Asteroids(void)

{

int index;

for (index=0; index<NUM_ASTEROIDS; index++)

{

// вращаем текущий астероид

Rotate_0bject ((object_ptr) &asteroids [index],

asteroids[index].angle);

} // конец цикла for

} // конец функции

///////////////////////////////////////////////////////

void main(void) {

_setvideomode(_VRES16COLOR); // 640х480, 16 цветов

// инициализируем поле астероидов

Create_Field{) ;

while(!kbhit())

{ // очищаем поле

Draw_Asteroids(ERASE) ;

// изменяем поле

Rotate_Asteroids();

Translate_Asteroids();

// рисуем поле

Draw_Asteroids(DRAW) ;

// небольшая задержка

Delay(500);

} // конец цикла while

// устанавливаем текстовый режим

_setvideomode( DEFAULTMODE);

} // конец функции main

Набрав, откомпилировав и запустив программу из Листинга 4.8, вы увидите на экране поле астероидов вместе со множеством разноцветных камней, отскакивающих от границ экрана (определение факта столкновения будет подробнее излагаться далее в этой главе, а также в главе одиннадцатой, «Алгоритмы, структуры данных и методология видеоигр»)

Теперь нам надо еще кое-что обсудить:

§          Первое, на что вы обратили внимание, это то, что образы слегка мелькают. Это связано с тем, что программа формирует изображение в тот же момент, когда происходит перерисовка экрана.

§          Экран — это множество линий, которые рисуются на мониторе слева направо и сверху вниз вашей видеокартой. Проблема заключается в том, что мы не можем изменять видеобуфер, пока на экране что-то рисуется. В пятой главе, «Секреты VGA-карт», мы обсудим рисование всего экрана целиком в отдельный буфер с последующим перемещением его в видеопамять;

§          Другая проблема, связанная с мерцанием, заключается в том, что мы используем графическую бибилотеку Microsoft С, которая не очень быстро работает. Вы должны понимать, что Microsoft не оптимизировал ее для высокой производительности и скорости работы;

§          Программа использует числа с плавающей запятой, которые впоследствии будут заменены числами с фиксированной запятой;

§          Вся программа совершенно неэффективна с точки зрения написания видеоигр. Все, что она делает, выполнено в классической, «книжной» манере. У разработчиков видеоигр есть правило номер 1: «Всегда есть способ сделать то, что кажется невозможным». Если б это было не так, то половина видеоигр вообще никогда не была бы написана, поскольку ПК не в состоянии обеспечить нужной производительности.

(Поверьте мне, DOOM — это лучший пример моим словам. Если бы я его не видел, то никогда не поверил бы, что такое возможно. Но, как мы знаем, DOOM существует, и это наилучший пример использования правильных методов для создания реального мира на компьютерном экране.)

Вращение, параллельное оси Х

Следующая матрица преобразований вращает точку (x,y,z) параллельно оси X:

Вращение, параллельное оси Y

Матрица преобразования, вращающая точку параллельно оси Y:

Вращение, параллельное оси Z

Матрица преобразования, вращающая точку параллельно оси Z;

Вращение трехмерного объекта

Последняя трансформация, о которой мы поговорим - это вращение. Вращение трехмерного объекта аналогично двухмерной ротации; необходимо только добавить третье измерение.

Временная синхронизация

Временная синхронизация означает привязку обеих машин к некоему общему таймеру, который может быть как внутренним, так и внешним. Как я уже говорил, необходимо, чтобы обе игры протекали в одном и том же темпе и каждое событие происходило на обоих компьютерах одновременно. Существует много путей для этого, но здесь приводятся только два из них:

§ Один путь состоит в обмене данными между компьютерами с определенный интервалом времени, который выбирается одинаковым для обеих машин. К примеру, машины производят обмен каждые 1/30 секунды. В результате система будет терять синхронизацию не более чем на 1/30 секунды.

§ Другой технический прием основан на ожидании посылающим компьютером подтверждения того, что сообщение принимающим ПК получено. Это показано на рисунке 14.9.

Первый компьютер передает свое состояние другому. .Как только вторая машина подтвердит получение этого сообщения и передаст свое состояние, ПК1 может продолжать работу. И запомните, что с точки зрения второго ПК все должно происходить наоборот. То есть после соединения компьютеров один из них получит сообщение первым и тут же вернет его назад - сообщение начнет ходить взад и вперед.

Этот метод имеет интересный побочный эффект: для сохранения состояния синхронизации компьютеры вынуждены работать с более низкой скоростью. Это происходит оттого, что максимальная задержка определяется не быстродействием ПК, а тем, как долго каждой из машин обрабатываются сообщения.

Прекрасно, теперь вы просто эксперты по коммуникациям. Это было не так уж и сложно, не правда ли? Даже если вы и не стали специалистом, то, по крайней мере, должны неплохо разбираться в этом вопросе и у вас появилось несколько технических приемов для решения возможных проблем. Перед тем как мы приступим к игре Net-Tank, я хочу сказать пару слов о модеме.

Время выполнения Алгоритма Художника

Алгоритм художника хорошо, но, к сожалению, медленно работает. В худшем случае, количество операций примерно равно O(n2), где n - количество многоугольников.

в жизнь идею компьютерной игры?

Как претворить в жизнь идею компьютерной игры? Приходилось ли вам, играя в свою любимую игру, мечтать о том, как можно было бы ее улучшить? Задумывались ли вы в процессе игры о том, как она устроена? Эта книга откроет вам путь к созданию собственных игр.

Вычисление линий для генерации

Поскольку мы сумели успешно заполнить таблицу значения наклонов, то теперь готовы ею воспользоваться для вычисления линий.

1. Находим позицию игрока для текущего отсечения лучей или рендеринга.

2. Вычисляем первое пересечение для каждого луча, который отсекается пересечением.

Помните, что игрок находится на плоской карте, которая используется для создания трехмерного образа. В нашем случае площадь мира составляет 16х16 ячеек, и каждая ячейка имеет размер 64х64 пикселя. Таким образом, мир имеет 1024х1024 виртуальных единиц измерения. Вне зависимости от позиции, игрок будет занимать несколько ячеек игрового пространства, поскольку «размер» самого игрока равен размеру ячейки. Эта позиция вычисляется простым делением глобальной позиции игрока, которая меняется от 0 до 1023 для Х и Y, на 64,или

ячейка_х = х_размерность / 64

ячейка_у = у_размерность / 64

где х_размерность и у_размерность находится в пределах от 0 до 1023.

Когда координаты текущей игровой ячейки будут вычислены, мы сможем найти ее пересечение с текущим лучом. Давайте рассмотрим математику для выполнения этих действий.

Вычисление масштаба

Теперь поговорим о масштабах. В виртуальном мире компьютера понятие масштаба превращается в понятие относительного масштаба. Таким образом, об этом можно говорить только в сравнении с чем-либо другим.

Для вычисления масштаба мы применяем сравнение между Х- и Y-пересечениями. Масштаб или высота вычисляется на основе ближайшего пересечения. Когда мы вычисляем масштаб битовой карты, мы можем использовать само расстояние:

масштаб = расстояние до пересечения

Это не всегда срабатывает: приближаясь, объекты становятся больше, но не уменьшаются при удалении. Тогда можно применить такую формулу:

масштаб = 1 / расстояние до пересечения

Это работает. Но результат надо умножить на некоторый коэффициент расстояния (или правдоподобия — как вам больше нравится).

масштаб = К / расстояние до_пересечения

где К стоит подобрать самостоятельно.

Вычисление оставшихся пересечений

После того как мы нашли первое пересечение для вертикальной и горизонтальной стены, можно найти следующую точку возможного пересечения — достаточно прибавить константы к текущей точке пересечения. Например, если координата Yi пересечения равна 100, то следующая точка Yi может быть рассчитана простым прибавлением числа 100.

В нашем случае каждая ячейка имеет размеры 64х64, и чтобы найти следующее пересечение мы используем следующие формулы:

Формула 6.4. Вычисление Х-координаты следующего возможного пересечения.

Следующее Xi = Xi + М х (ширина ячейки)

Формула 6.5. Вычисление Y-координаты следующего возможного пересечения.

Следующее Yi = Yi + М х (высота ячейки)

где высота и ширина ячейки равна 64.

Это не так плохо: вычисление следующего возможного пересечения требует двух умножений и двух сложений. Помните, отсечение лучей должно выполняться максимально быстро, а иначе в нем нет смысла.

После вычисления следующей возможной точки мы проверяем, есть ли там что-то на самом деле. Если есть, то мы вычисляем дистанцию до этого пересечения. Дистанция используется позже, для трехмерного рендеринга. Если же пересечения нет, то мы продолжаем отсечение.

Вычисление расстояния

Теперь, когда мы нашли пересечение с объектом, встает вопрос о том, как вычислить расстояние до него. Поскольку мы нашли точку пересечения, то можем найти и расстояние от этой точки до позиции игрока. Это расстояние нам нужно для двух вещей:

Чтобы узнать тип пересечения (вертикальное или горизонтальное);

§ Чтобы выяснить масштаб стен.

Формула 6.6. Теорема Пифагора.

Мы можем использовать для этого теорему Пифагора;

Н =sqrt (х2 + у2)

Это прекрасная формула, но ужасно сложная для ПК, поскольку вычисление квадратного корня — процесс весьма медленный и долгий. Мы, конечно, можем использовать табличное представление функции квадратного корня, но и в этом нет ничего хорошего. Есть другой, более простой способ найти удаление точки пересечения от игрока, если вычислить координаты точек и найти sin © и cos ©.

Давайте посмотрим на рисунок 6.26.

Поскольку мы уже вычислили точки вертикального и горизонтального пересечения, мы можем воспользоваться известным правилом, чтобы найти синус и косинус угла наклона:

§ Угол наклона луча (он у нас есть);

§ Длина гипотенузы (мы ее хотим найти);

§ Длина сторон треугольника (который мы имеем).

Назвав переменные так же, как они обозначены на рисунке 6.26, напишем формулы для вычисления длины- гипотенузы (или, что то же самое - искомого расстояния).

Формула 6.7. Вычисление расстояния до точки Х-пересечения.

расстояние = (Xi

- Хр) х cos-1

Формула 6.8. Вычисление расстояния до точки Y-пересечения.

расстояние = (Yi

- Yp) x

sin-1

где А - это угол луча, который рассматривается в настоящее время. В программе это просто индекс от 0 до 1920 для таблицы вычисленных значений sin-1 и cos-1.

Это может показаться громоздким, но если это правильно написать и оптимизировать, то процесс будет занимать несколько миллисекунд. После того как расстояние будет вычислено, встает вопрос, что ближе, а что дальше на экране.

Вычисление точки первого пересечения

Существует множество способов описания прямой: от параметрического до функционального. Мы будем рассчитывать нашу прямую с помощью функции, описывающей линию.

формула 6.2. Вычисление первой Y-координаты пересечения.

(Yi – Yp)

------------- = M

(Xi – Xp)

Yi = M * (Xi – Xp) + Yp

где (Xi,Yi) - точки пересечения линии и (Xp,Yp) — позиция игрока. После некоторых алгебраических преобразований получаем:

Формула 6.3. Вычисление первой Х-координаты пересечения.

Xi = M-1 * (Yi – Yp) + Xp

Для нахождения первого пересечения текущего луча нам надо выполнить только два умножения и сложение. Не так плохо. Мы обязательно это оптимизируем, но сделаем это позже. Переменная М — это величина наклона, которую мы уже вычислили и занесли в таблицу наклонов.

Единственное, что может нас расстроить в этих преобразованиях, это их рекурсивность: каждое преобразование требует предварительного вычисления Другого. Это несколько затруднительно. Но вы можете заметить, что Xi в первом равенстве на самом деле означает «первая граничная вертикальная линия», a Yi во втором выражении означает «первая граничная горизонтальная линия». В этом и заключена изюминка метода отсечения лучей для квадратных матриц. Далее, мы знаем, что луч пересекается с каждой из ячеек в вертикальном и горизонтальном столбце. Рисунок 6.24 поясняет это, Если мы однажды вычислим первое пересечение, то сможем найти и все остальные пересечения с лучом, а также конец его траектории.

Прежде чем рассказать вам о поиске остальных пересечений, я хочу отметить, что каждый: луч может иметь пересечения как с вертикальной, так и с горизонтальной асимптотами, и мы должны вычислять эти пересечения.

Некоторые, программисты любят это делать за два прохода: в первом вычисляются все возможные горизонтальные пересечения, а во втором — все вертикальные пересечения. Рисунок 6.25 демонстрирует эту идею.

Это нормально, но я предпочитаю делать это одновременно. Время выполнения обоих методов одинаково, а остальное - дело вкуса. Есть еще одна деталь в работе с пересечениями, для каждого из них (включая самое первое) мы проверяем наличие непрозрачного объекта. Мы должны посмотреть во все стороны от пересечения и попробовать его заметить. Направление просмотра зависит or нашего положения. Если мы находим объект, то останавливаемся и вычисляем дистанцию до пересечения (мы научимся это делать позже). Если мы не обнаруживаем пересечений, то просто продолжаем вычисления до тех пор, пока луч не упрется в какой-либо объект или не выйдет за границы нашего игрового мира.

Взаимодействие с пользователем в видеоиграх

Компьютерные игры не были бы так азартны, если бы мы не могли влиять на разворачивающиеся в них события. Основная идея видеоигры состоит в возможности, взаимодействия с «виртуальным миром» в реальном масштабе времени. Когда видеоигры только появились, они имели совершенно убогий интерфейс - многие из них управлялись только парой клавиш.

Но время шло и появлялись новые устройства ввода. Фирма Atari и некоторые другие начали выпускать игры, управляемые джойстиками и более хитрыми устройствами типа «пилотского штурвала». Сегодня для ПК создано множество устройств - плод кропотливых теоретических и практических инженерных разработок.

Как создатели видеоигр, мы должны уделять пристальное внимание работе с устройствами ввода. Люди, играющие в наши игры, должны иметь удобный и надежный интерфейс для изучения созданного нами мира. Если же взаимодействие с системой неудобно и сложно, не поможет ни красивая музыка, ни видеоэффекты — людей не привлечет игра, которой они не смогут управлять. Надо сказать, что сейчас очень удачное время для тех, кто собирается заняться видеоигорным бизнесом. Сегодня мы можем выделить среди пользователей ПК несколько больших групп. Например:

Большинство имеет компьютеры 386 и 486;

§ У большинства есть, как минимум, VGA-карты и многие располагают звуковыми картами;

§ Наконец, благодаря президенту Microsoft Билу Гейтсу и большой популярности оболочки Windows, практически у всех есть мыши.

Можно задать вопрос: «А имеет ли предполагаемый игрок джойстик?» Ответ будет менее определенным: «кто-то имеет, а кто-то — нет». Многие все же предпочитают клавиатуру. Неважно, какое из устройств используется, мы должны добиться, чтобы его применение было для игрока почти интуитивным. Не в нашей власти выбирать, какое из устройств должно поддерживаться игрой. Мы обязаны научиться работать с любым из них. В данном случае мы должны стать рабами тех, для кого пишем игры, хотя наша философия и привычки (в выборе устройств ввода) могут сильно отличаться от привычек наших игроков.

Теперь без лишних слов начнем с джойстика.

Зачем нам нужен ассемблер при написании игр?

Даже для таких компьютерных богов, как Microsoft и Borland, сегодня ассемблер намного быстрее программ на Си. Я помню дни, когда все игры были написаны целиком на ассемблере. Вы можете себе это представить? К счастью сейчас у нас есть куча ученых и программистов, которые заняты разработкой компиляторов. Эти компиляторы дают код, не многим хуже ассемблерного. Но, к сожалению, даже компиляторы чуть-чуть не дотягивают до идеала. Вот почему нам обычно приходится последние пять процентов делать своими руками. Мы должны применять ассемблер для рисования точек, линий, выполнения заливок, наложений и т. д. Мы вынуждены его применять там, где нужна сверхскорость - в графике.

Существует несколько способов включения ассемблера в наши программы:

Можно написать на ассемблере отдельную функцию и вызывать ее из Си. Мы используем этот способ в критичных по времени выполнения участках программы;

§ Мы можем использовать такую штуку, как встроенный ассемблер. Он позволяет использовать инструкции ассемблера наравне с Си-кодом. Это неоценимая находка для разработчика видеоигр, поскольку вам не надо использовать кучу промежуточных утилит и создавать массу независимых текстов программ. Кроме того, встроенный ассемблер здорово экономит ваше время.

Прежде чем двинуться дальше, я хочу предостеречь вас от одной из крайностей - не надо пытаться написать на ассемблере все. Используйте его экономно и только тогда, когда он действительно нужен. В противном случае ваш код будет довольно сложен и непереносим (кстати, в том же самом DOOM'e на ассемблере написано всего несколько процедур, а все остальное — это эффективный Си-код). Если же вам надо написать более двух тысяч строк ассемблера, то лучшим решением будет пересмотр применяемого вашего алгоритма.

В этой главе мы изучили

В этой главе мы изучили некоторые нетривиальные приемы управления работой персонального компьютера. Мы узнали, как работает таймер, как можно использовать прерывания (включая и клавиатурные) и многое другое.
Мы научились писать обработчики прерываний на языке Си и регистрировать их в таблице векторов прерываний. Кроме того, мы узнали много полезного о том, как при помощи автономных функций и функций ответа можно организовать на персональном компьютере синхронизацию программы и обработку наступления определенных событий.
И, в конце концов, мы использовали полученные знания Для написания нескольких программ, которые брали на себя управление компьютером - одна из этих программ даже не пожелала вернуть управление обратно!

Закон Ламберта

Давайте поговорим об отражении и интенсивности. Если источник света направлен на поверхность под некоторым углом и наблюдатель смотрит на поверхность параллельно нормали, то интенсивность света изменяется в соответствии с законом Ламберта:

Id = Ii Kd cosQ 0<= Q <= Pi/2

где:

• Id - результирующая интенсивность;

• Ii - интенсивность источника;

• Kd — коэффициент отражения материала;

• Q - угол между нормалью и направлением освещения.

Выражаясь нормальным языком, это означает, что отражение света возрастает, когда направление на источник света становится коллинеарным с нормалью к отражающей поверхности, или, иными словами, когда отражающая поверхность размещена прямо за источником света.

Закон обратных квадратов

Интенсивность света уменьшается обратно пропорционально квадрату расстояния до источника. То есть чем дальше вы находитесь от источника, тем меньше его интенсивность. Кстати, все это звучит очень правдоподобно.

Все неуказанные номера функций являются

Все неуказанные номера функций являются устаревшими.
Функция № 1: DigPlay
Функция DigPlay исполняет 8-битный оцифрованный звук. Она является базовой функцией DIGPAK для исполнения звуковых эффектов. Прикладная программа создает структуру звуковых данных, описывая положение звука в памяти и его продолжительность. Функция DigPlay может модифицировать содержимое звукового буфера. Поэтому если вам необходимо исполнить звуковой эффект более одного раза, используйте комбинацию функций MassageAudio и DigPlay2. Вы также можете использовать DigPlay для воспроизведения звука с разным разрешением с компакт-дисков и даже для его записи. Универсальность данной функции объясняется тем, что интерфейс пакета программ DIGPACK развивался в течение нескольких лет и изначально содержал только одну эту функцию. Для обеспечения совместимости сверху вниз, эта функция сохранила прежние возможности, получив расширенные установки различных режимов воспроизведения и записи.
Прототип этой функции находится в файле DIGPLAY.H. Реализация функции содержится в файле DIGPLAY-OBJ, объектном файле, созданном из файла DIGPLAY.ASM. Вы можете использовать либо интерфейсные функции, либо напрямую вызывать прерывание 66h.
Вход:    AX=688h    Номер команды
DS:SI        *Реальный режим*
   Указатель на звуковую структуру, описывающую звуковой эффект.
ESI *Прямая адресация*
В случае использования 32-разрядной адресации, ESI указывает на 32-разрядный адрес звуковой структуры в первом мегабайте адресного пространства. Будет преобразован драйвером DIGPAK в допустимый адрес СЕГМЕНТ:СМЕЩЕНИЕ.
Выход: Ничего
Функция № 2: SoundStatus
Данная функция проверяет текущее состояние звукового драйвера и возвращает номер версии для драйверов версии 3.1 и выше. Она используется для запроса текущего состояния исполнения звукового эффекта. Если в настоящий момент звуковой эффект воспроизводится, в регистре АХ будет возвращена 1. Данная функция также используется для определения версии звукового драйвера DIGPAK, числовое значение которой помещается в регистр ВХ.

Это справедливо Для драйверов версий 3.1 и выше. Для получения этого значения вы также Можете использовать функцию ReportVersionNumber.
Вход:    AX          =689h
Выход: АХ          =0        Звук не исполняется.
=1        В настоящий момент исполняется звуковой эффект.
ВХ=         Начиная с версии 3.1 вызов функции SoundStatus возвращает в регистре ВХ номер версии. Номер версии возвращается в десятичном формате и умножен на 100, то есть значение 310 соответствует версии 3.10. Версии ниже 3.1 ничего невозвращают в регистре ВХ, так что вы должны обнулить его перед проверкой номера версии. Если ВХ остался нулевым, значит версия загруженного драйвера DIGPAK меньше, чем 3.1.
Функция № 3: MassageAudio
Функция преобразует звуковые данные в выходной формат аппаратного обеспечения. Данные будут преобразованы в необходимый аппаратно-зависимый формат в соответствии с заголовком структуры. Например, некоторые устройства не позволяют воспроизводить звук непосредственно в беззнаковом 8-битном формате. После переформатирования содержимого памяти, вы можете без перезагрузки данных использовать функцию DigPlay2 столько раз, сколько это необходимо.
ВХОД: AX=68Ah
DS:SI           *Реальный режим* Указатель на звуковую структуру, описывающую звуковой эффект.
ESI          *Прямая адресация* В случае использования 32-разрядной адресации, ESI указывает на 32-разрядный адрес звуковой структуры в первом мегабайте адресного пространства. Будет преобразован драйвером DIGPAK в допустимый адрес СЕГМЕНТ:СМЕЩЕНИЕ.
Функция № 4: DigPlay2
Функция исполняет звуковые данные, преобразованные в необходимый аппаратно-зависимый формат. В сочетании с MassageAudio она позволяет воспроизводить звуковые данные, не изменяя содержимого звукового буфера.
ВХОД: АХ-68ВП
DS:SI        * Реальный режим* Указатель на звуковую структуру, описывающую звуковой эффект.
ESI          *Прямая адресация* В случае использования 32-разрядной адресации, ESI указывает на 32-разрядный адрес звуковой структуры в первом мегабайте адресного пространства.

Будет преобразован драйвером DIGPAK в допустимый адрес СЕГМЕНТ:СМЕЩЕНИЕ.
ВЫХОД: Ничего
Функция № 5: AudioCapabilities
Данная функция сообщает о возможностях аппаратного обеспечения. Она возвращает информацию от резидентного драйвера DIGPAK об ограничениях и специфических особенностях платы в виде слова состояния, которое вы можете легко проанализировать.
ВХОД: АХ=68Ch ВЫХОД: АХ=Бит 0 ->     1 - поддерживается фоновое воспроизведение
0 - драйвер воспроизводит звук только как основной процесс.
Бит 1->   1 - исходные данные должны быть преобразованы для выходного устройства;
0 - устройство способно воспроизводить неформатированные 8-битовые беззнаковые звуковые данные
Бит 2 ->      1 - устройство может воспроизводить звук только с фиксированной частотой, но звуковой драйвер способен понизить частоту входных данных
0 - устройство способно воспроизводить звук с указанной пользователем частотой.
(Замечание: Вы в любом случае можете воспроизводить звуковой фрагмент с нужной частотой, драйвер способен понизить частоту входных данных. Однако повышение частоты пока не поддерживается.)
Бит 3 ->      1 — устройство использует вектор прерывания таймера во время воспроизведения звука.
Бит 4 ->     1 — драйвер поддерживает разделение таймера (не доступно в защищенном режиме).
Бит 5->      1 — поддерживается режим ожидания.
Бит б->      1 — поддерживается режим стереопанорамы.
Бит 7->      1 - поддерживается воспроизведение 8-битного РСМ-стереозвука.
Бит 8->      1 — поддерживается запись звука.
Бит 9->      1 - поддерживается режим обратной записи DMA.
DX =        Если драйвер может воспроизводить данные только с определенной частотой, в регистре DX содержится значение этой частоты.
Функция № 8: StopSound
Функция немедленно останавливает воспроизведение музыкального фрагмента.
ВХОД: AX=68Fh
ВЫХОД: Ничего       Вызывает немедленное прекращение воспроизведения текущего музыкального фрагмента.
Функция № 12: SetTimerDivisorRate
Эта функция не работает в защищенном режиме.

Она позволяет прикладной программе информировать драйвер DIGPAK, использующий таймер, о перепрограммировании частоты прерываний таймера 8253. Данная функция используется только в реальном режиме, так как ни один из базирующихся на прерывании таймера драйверов DIGPAK не работает в защищенном режиме. Если ваша компьютерная игра перепрограммировала таймер 8253 на новую частоту, вы должны сообщить об этом драйверу DIGPAK. Для того чтобы обеспечить воспроизведение музыкального фрагмента, драйвер DIGPAK, использующий таймер, должен перепрограммировать 8253 на очень высокую частоту- По умолчанию DIGPAK считает исходную частоту прерываний таймера равной стандартной (18.2 раза в секунду) и устанавливает это значение после завершения музыкального эффекта. Однако данная функция позволяет вам поставить драйвер DIGPAK в известность об изменении базовой частоты. В результате этого драйвер будет обслуживать программу прерываниями таймера с указанной частотой, а после воспроизведения звукового эффекта драйвер установит таймер на эту частоту.
ВХОД: AX=693h
DX=         Делитель частоты таймера. Драйверы, базирующиеся на прерываниях от таймера, способны обслуживать прикладную программу прерываниями от таймера с заданной делителем частотой независимо от частоты прерываний, необходимой для воспроизведения звукового эффекта. Реально частота прерываний будет стремиться к заданной величине. Для восстановления стандартной частоты прерываний (18.2 раза в секунду) в регистре DX следует задать 0.
ВНИМАНИЕ!!! Если вы перепрограммируете таймер в своей программе, при выходе из нее обязательно восстановите нормальное значение частоты прерываний — 18.2 раза в секунду.
ВЫХОД: Ничего
Функция № 14: PostAudioPending
Данная функция позволяет вам поместить в очередь второй музыкальный фрагмент. Начиная с версии DIGPAK 3.0, приложение может задать второй музыкальный фрагмент, который должен быть воспроизведен сразу по окончании воспроизведения текущего фрагмента. Этот метод, называемый двойной буферизацией, позволяет вашей прикладной программе осуществлять очень сложное манипулирование звуком.

Используя двойную буферизацию, вы можете производить программное микшироваиие и (или) подкачивать длинное музыкальное произведение с диска, или из расширенной памяти EMS. В демонстрационной программе PEND.C показано, как можно исполнить по частям большой звуковой клип. Модифицируя эту демонстрационную программу, вы можете воспроизводить звуковые эффекты с диска, или выполнять программное микширование, добавляя набор звуковых эффектов в основной музыкальный поток.
ВХОД: AX=695h
DS:SI        *Реальный режим*. Указатель на звуковую структуру, описывающую звуковой эффект.
ESI          *Прямая адресация* В случае использования 32-разрядной адресации, ESI указывает на 32-разрядный адрес звуковой структуры в первом мегабайте адресного пространства. Будет преобразован драйвером DIGPAK в допустимый адрес СЕГМЕНТ:СМЕЩЕНИЕ.
ВЫХОД: АХ=0        Началось воспроизведение фрагмента.
АХ=1        Фрагмент поставлен в очередь на воспроизведение.
АХ=2        В очереди уже имеется фрагмент, поэтому данный фрагмент в очередь не поставлен.
Функция № 15: AudioPendingStatus
Функция позволяет получить текущий статус состояния двойного буфера функции PostAud io Pending. Система с двойной буферизацией может находиться в одном из трех состояний. В состоянии 0 никакой звуковой фрагмент не воспроизводится. В состоянии 1 музыкальный фрагмент воспроизводится, но в очереди фрагментов больше нет (это означает, что пришло время поместить-в очередь следующий звуковой фрагмент). И, наконец, последний вариант — первый фрагмент воспроизводится, а второй уже находится в очереди, в этом случае никаких действий от прикладной программы не требуется,
ВХОД: АХ=696Ь ВЫХОД: АХ=0        Никакой фрагмент не воспроизводится.
АХ=1        Один фрагмент воспроизводится, другой фрагмент ожидает своей очереди.
АХ=2        Звуковой фрагмент воспроизводится, но очередь пуста.
Функция № 16: SetStereoPan
В настоящее время эта функция поддерживается только несколькими устройствами, например, Sound Blaster Pro.

Вы можете вызывать AudioCapabilities для проверки возможности использования текущим драйвером режима стереопереходов. На некоторых стереозвуковых платах, таких как Sound Blaster Pro, вы можете управлять раскладкой монозвукового эффекта по стереоканалам. С помощью вызова данной функции вы указываете звуковой плате процентное •соотношение громкости вашего фрагмента для правого и левого динамиков. Вы можете вызывать эту функцию когда угодно, даже во время воспроизведения, чтобы перемещать звук от динамика к динамику. Это позволяет вам разнообразить вашу игру захватывающими и потрясающими эффектами.
ВХОД: AX=697h
DX=         Процентное соотношение громкости по каналам:
0 — 100% на правый динамик.
64 — 50% по обоим динамикам.
127 — 100% на левый динамик.
ВЫХОД: АХ=0        Команда проигнорирована, драйвер не поддерживает стереопереходов.
АХ=1        Команда выполнена.
Функция № 17: SetPlayMode
функция позволяет установить режим записи/воспроизведения для резидентного драйвера DIGPAK. Из-за того, что, появившись в 1987 году, DIGPAK обеспечивал всего лишь одну функцию (воспроизведение звукового эффекта), независимая функция была наиболее простым способом расширения возможностей драйвера с одновременным сохранением совместимости сверху вниз. С помощью данной функции вы можете задать разрешение, при котором будет выполняться воспроизведение или запись звукового фрагмента.
ВХОД: AX=698h
DX==         Режим воспроизведения. DX       =0 ->     8-разрядный РСМ.
=1 ->     8-разрядный стерео-РСМ (правый/левый).
=2 ->     16-разрядный РСМ.
=3 ->      16-разрядный стерео-РСМ.
После изменения режима воспроизведения все функции DIGPAK работают точно так же, как и раньше, но ожидают данные в установленном формате. 8-разрядный стерео-РСМ состоит из пар беззнаковых данных для обоих каналов. Поддерживается платами Stereo FX и Sound Blaster Pro. Все 16-разрядные данные являются знаковыми и в случае стереозвука их знак определяет правый или левый канал записи/воспроизведения.

ВЫХОД: АХ   = 1       Режим установлен.
АХ = 0      Режим не поддерживается данным драйвером.
Функция № 18: Адрес флага ожидания и адрес «семафора» DIGPAK
Эта функция сообщает прикладной программе адрес в памяти, по которому расположен внутренний флаг ожидания драйвера DIGPAK. Этот метод называется «семафором и позволяет программе постоянно отслеживать состояние флага, не выполняя вызова функции. По изменению состояния этого флага, ваша программа может принимать решение о помещении следующего звукового фрагмента в очередь ожидания.
int far *ReportPendingAddress(void);
Сообщает дальний адрес флага ожидания. Если ячейка памяти по этому адресу содержит значение 1, это означает, что следующий фрагмент все еще ожидает своей очереди. Когда значение ячейки становится равным 0, ваша программа может начать загрузку следующего фрагмента в двойной буфер. Использование «семафора» для определения момента загрузки следующего фрагмента предпочтительнее, чем вызов функции AudioPendingStatus.
int far *ReportSemaphoreAddress(void) ;
Сообщает адрес «семафора» DIGPAK. Возвращаемый указатель является дальним указателем на ячейку памяти внутри драйвера DIGPAK. Если значение не нулевое, то DIGPAK находится в активном состоянии и вы не должны в это время вызывать какие бы то ни было функции DIGPAK по аппаратному прерыванию, так как это, возможно, прервет исполнение кода самого драйвера.
ВХОД: AX=699h
ВЫХОД: AX:DX      Дальний адрес флага ожидания.
BX:DX      Дальний адрес «семафора» DigPak. (При использовании DIGPAK.ASM в 32-разрядном режиме адресации, возвращаемый адрес будет преобразован в допустимый 32-разрядный адрес.)
Функция № 19: Установка режима записи
Функция позволяет вам установить DIGPAK в режим записи или воспроизведения звука. Вызов функции DigPlay после установки режима записи, обеспечивает запись звука в указанный буфер памяти. Функция поддерживается только для карт Sound Blaster.
ВХОД: AX-69AI1
DX=0 Включить режим записи.
DX=1       Выключить режим записи.

ВЫХОД: АХ=0        Драйвер не поддерживает запись звука.
АХ=1        Режим записи звука установлен.
Функция № 21: Установка режима обратной записи DMA
Функция позволяет включить режим обратной записи DMA. В идеале было бы достаточно использовать функцию PostAudioPending. Однако большинство моделей звуковых карт не позволяют гладко проиграть две звуковые последовательности одну за другой. И хотя фирма Creative Labs уже продала свыше двух миллионов карт Sound Blaster без этого недостатка, другие звуковые платы по-прежнему не способны обеспечить ровную стыковку двух звуковых фрагментов. Единственный способ обойти данную проблему состоит в использовании метода обратной записи DMA. В идеале функция PostAudio Pending должна была бы автоматически использовать этот метод, но это заняло бы слишком много времени для изменения всех имеющихся драйверов. Метод, с помощью которогб DIGPAK поддерживает режим обратной записи, достаточно прямолинеен, но пока я придумываю что-нибудь получше, вы вполне можете им воспользоваться.
Посмотрев на демонстрационную программу PEND.C, вы увидите пример того, как вместо PostAudioPending используется метод обратной записи DMA в том случае, если это поддерживается звуковой картой. Вы можете свободно использовать этот подход к реализации двойной буферизации в своих программах.
Обычно во время воспроизведения музыкального фрагмента звуковая карта осуществляет прямой доступ в память, который прерывается программой по окончании воспроизведения звука. Такой метод используется для исполнения одного фрагмента за один раз и это является стандартным режимом для вызовов функций DIGPAK. При автоматической инициализации прямого доступа в память, по достижении конца звукового фрагмента контроллер прямого доступа в память немедленно возвращается в начало буфера; он никогда самостоятельно не заканчивает воспроизведение. Следовательно, если ваш фрагмент — это слово «Привет!» и вы инициировали прямой доступ в память, то будете слышать «Привет!» непрерывно до тех пор, пока не прервете воспроизведение.

Как же использовать подобное поведение контроллера прямого доступа в память для двойной буферизации? Вначале вы должны выбрать фиксированный размер буфера передачи, например, 2 килобайта. Затем, если ваш буфер размером 2К, вы должны зарезервировать двойной буфер, то есть 4К. Теперь, начав воспроизведение этого четырехкилобайтного буфера, вы должны следить за тем, какую половину буфера в данный момент проигрывает DIGPAK. Каждый раз, когда DMA пересекает границу 2К, вам следует записать следующие 2К позади текущей позиции воспроизведения! Вот почему этот метод получил название обратной записи. Фактически, вы записываете данные позади текущей передачи данных с использованием прямого доступа в память. Чтобы жизнь не показалась вам такой уж простой, помните, что вы не можете использовать любые 4К для подобного буфера. Он не может пересекать границ страницы. Границы страниц располагаются через каждые 64К в первом мегабайте адресного Пространства компьютера. Поэтому DIGPAK содержит функцию, которая позволяет выяснить, не пересекает ли выбранный вами буфер одну из таких границ. если да, то просто выберите следующие 4К для вашего буфера, они уже точно пересекут границу.
Все это звучит достаточно запутано... но так оно и есть. Именно поэтому я и предоставил в ваше распоряжение простую программу PEND.C. Вы можете использовать ее как прообраз для своих функций воспроизведения звука. Используя прямой доступ в память и двойную буферизацию, вы сможете подкачивать звуковые данные с диска, осуществлять программное микширование в реальном времени и создавать звуковое сопровождение для фильмов и FLIC-файлов.
ВХОД: АХ = 69СЬ
DX=0       Выключить режим обратной записи.
DX=1        Включить режим обратной записи.
ВЫХОД: АХ=0        Режим обратной записи не поддерживается драйвером.
АХ=1        Режим обратной записи установлен.
Функция № 22: Значение счетчика прямого доступа в память
Функция возвращает текущее значение счетчика при прямом доступе в память. Другими словами, если вы начали передачу из буфера в 4К, в процессе воспроизведения счетчик будет изменяться от 4097 до 0.

Отслеживая значения счетчика, вы можете определить момент, когда следует заполнять следующую половину буфера. В программе PEND.C показано, как это сделать на практике.
ВХОД: AX=69Dh
ВЫХОД: АХ= Текущее значения счетчика (значение убывает, а не возрастает).
Функция № 23: Проверка буфера прямого доступа в память
Функция позволяет проконтролировать, не пересекает ли выбранный вами буфер прямого доступа в память грашщ страницы. Пример использования этой функции приведен в программе PEND.C.
ВХОД: AX=69Eh
ES:BX       *Реальный режим* Указатель на звуковую структуру, описывающую звуковой эффект.
ЕВХ         *Прямая адресация* В случае использования 32-разрядной адресации, ЕВХ указывает на 32-разрядный адрес звуковой структуры в первом мегабайте адресного пространства. Будет преобразован драйвером DIGPAK в допустимый адрес СЕГМЕНТ: СМЕЩЕНИЕ.
СХ = Размер буфера. ВЫХОД: АХ=1        Блок не пересекает границу страницы. АХ=0        Блок пересекает границу страницы.
Функция № 24: Установка громкости при импульсно-кодовой модуляции
Функция, реализована только для нескольких звуковых карт. Она позволяет установить для карты общую относительную громкость звука.
ВХОД: AX=69Fh
ВХ =         Громкость левого канала (или обоих для моно) 0-100.
СХ =         Громкость правого канала (или обоих для моно) 0-100.
ВЫХОД: АХ=1        Громкость установлена.
АХ=0        Устройство не поддерживает установку громкости.
Функция № 25: SetDPMIMode
Функция информирует драйвер DIGPAK о 32-разрядной адресации. Поскольку оригинальные драйверы DIGPAK предполагалось использовать только в реальном режиме, я не задумывался о возможности другой адресации. (Первые драйверы DIGPAK разрабатывались в 1987 году, поэтому в этом нет ничего удивительного.) Из-за того, что многие функции DIGPAK используют комбинацию регистров сегмента и смещения для формирования адреса, это порождает определенные проблемы в защищенном режиме. В защищенном режиме сегментные регистры являются селекторами и сформировать из них адрес реального режима трудно.

После вызова этой функции, DIGPAK будет знать, что он активизирован прикладной программой для защищенного режима и будет реагировать на полный 32-разрядный адрес в ESI, а не на комбинацию DS:SI. Процесс трансляции адреса автоматически обеспечивается интерфейсом нижнего Уровня DIGPLAY.ASM, находящимся в подкаталоге программ для защищенного режима.
ВХОД: АХ=6А0h
DX=   Режим включен/выключен (1/0). ВЫХОД: Ничего
#*****************************************************************
#***** DigPlay, компонуемый интерфейс Digitized Sound Package ****
#*****************************************************************
DIGPLAY.H Компонуемый интерфейс реального режима. Все процедуры имеют прототипы и используют имена сегментов, пригодные для любой модели памяти.
#ifndef LOADABLE_DRIVERS
ftdefine LOADABLE_DRIVERS 1// условная компиляция
#endif
/* битовые флаги возможностей драйвера     */
/* возвращаются функцией AudioCapabilities */
#define PLAYBACK       1   // бит 0, возможно воспроизведение звука
// в фоновом режиме
#define MASSAGE        2
// бит 1, данные преобразованы
//в аппартно-эависимый формат
#define FIXEDFREQ      4   // бит 2, драйвер воспроизводит звук
// только с фиксированной частотой
#define USESTIMER      8   // бит 3, драйвер использует таймер
#define SHARESTIMER   16   // бит 4, таймер может быть использован
// совместно (бета-версия!!!)
#define LOOPEND       32   // бит 5, поддерживается цикличность и
// очередь ожидания (бета-версия!!!)
#define STEREOPAN     64   // бит 6, поддерживаются стереопереходы
#define STEREOPLAY   128   // бит 7, поддерживается 8-разрядный
                        // РСМ-звук
#define AUDIORECORD 256   // бит 8, поддерживается запись звука
#define DMABACKFILL 512   // бит 9, поддерживается режим обратной                             // записи DMA
#define PCM16      1024   // бит 10, поддерживается 16-разрядный
// звук
#define PCM16STEREO 2048   // бит 11, поддерживается 16-разрядный

// стереозвук
typedef struct
{ char far *sound;            // адрес звуковых данных
unsigned short sndlen;     // длина звуковых данных
short far *IsPlaying;       // адрес флага состояния
short frequency;            // частота воспроизведения }SNDSTRUC;
extern short far cdecl DigPlay (SNDSTRUC far *sndplay) ;
// 688h -> воспроизведение 8-разрядного оцифрованного звука
extern short far cdecl SoundStatus (void);
// 689h -> сообщает состояние звукового драйвера
extern void far cdecl MassageAudio (SNDSTRUC far *sndplay);
// 68Ah -> преобразует цифровой звук в аппаратнозависимый формат
extern void far cdecl DigPlay2 (SNDSTRUC far *sndplay);
// 6SBh -> воспроизведение звука в аппаратноэависимом формате
extern short far cdecl AudioCapabilities (void);
// 68Ch -> сообщает информацию о возможностях драйвера
extern short far cdecl DigPakIdentityString (char far *str) ;
// 68Ch -> копирует в заданный буфер идентификатор драйвера
// звука и возвращает длину скопированной строки
extern void far cdecl StopSound (void) ;
// 68Fh -> останавливает воспроизведение звука
extern short far cdecl PostAudioPending (SNDSTRUC far *sndplay);
#define NOTPLAYING О // звук не воспроизводится
#define PLAYINGNOTPENDING 1 // звук воспроизводится, очередь пуста
#define PENDINGSOUND       2 // звук воспроизводится, следующий
// фрагмент ожидает своей очереди
extern short far cdecl AudioPendingStatus (void);
#define FULLRIGHT           0
#define FULLLEFT            127
#define FRONTANDCENTER      64
extern short far cdecl SetStereoPan(short panvalue);
// 0 - 127, 0 - 100% правый канал
#define PCM_8_MONO      О
#define PCM_8_STEREO   1
#define PCM_16_MONO 2 #define PCM_16__STEREO        3
extern short far cdecl SetPlayMode (short playmode);
// 0 - режим не поддерживается
// 1— режим поддерживается
extern short far cdecl SetRecordMode(short mode);
// устанавливает режим записи звука
extern short far * far cdecl PendingAddress (void);
// сообщает дальний адрес флага ожидания.

Если ячейка памяти по
// этому адресу содержит значение 1, это означает, что следующий
// фрагмент все еще ожидает своей очереди. Когда значение ячейки
// становится равным 0, ваша программа может начать загрузку
// следующего фрагмента в двойной буфер. Использование "семафора"
// для определения момента для загрузки следующего фрагмента
// предпочтительнее, чем вызов функции AudioPendingStatus.
extern short far * cdecl ReportSemaphoreAddress(void);
// сообщает адрес семафора DIGPAK. Возвращаемый указатель является
// дальним указателем на ячейку памяти внутри драйвера DIGPAK. Если
// значение не нулевое, то DIGPAK находится в активном состоянии и
// вы не должны в это время вызывать какие бы то ни было функции
// DIGPAK по аппаратному прерыванию, так как это, возможно, прервет
// исполнение кода самого драйвера.
extern void far cdecl SetTimerDivisorRate (short rate) ;
// устанавливает делитель частоты для таймера
// Если ваша программа перепрограммировала таймер 8253 на новую
// частоту, вы должны сообщить об этом драйверу DIGPAK.
// Не забудьте восстановить стандартную частоту после завершения
// работы программы.
extern short far cdecl ReportVersionNumber (void);
// сообщает версию драйвера DIGPAK
// Номер версии возвращается умноженным на сто, то есть значение
// 310 соответствует версии 3.1. Драйверы версий младше 3.1 не
// поддерживают данную функцию, поэтому нулевое значение означает,
// что версия загруженного драйвера DIGPAK меньше, чем 3.1.
extern short far cdecl SetBackFillMode (short mode);
// Устанавливает режим обратной записи DMA. Возвращает 1, если
// режим.установлен, и 0, если драйвер не поддерживает этот режим.
extern unsigned short far cdecl ReportDMAC (void);
// сообщает текущее значение счётчика DMA
extern short far cdecl VerifyDMA (chac far *data, short length);
// Проверяет, не пересекает ли буфер границ страницы. Возвращает 1,
// если граница не пересекается, и 0, если буфер пересек границу.
extern void far cdecl NullSound (char far *sound, short sndlen, short null) ;
/* Дополнительные функции */
extern void far cdecl WaitSound (void);
// ожидание окончания воспроизведения звука
extern short far cdecl Checkin (void);
// Загружён ли драйвер. 1 - да; О - нет.
/**** Внимание!!! Если вы используете LOADABLE_DRIVERS, то должны
обеспечить доступ к функциям распределения памяти и к DOSCALLS.OBJ.
extern short far cdecl InitDP (short segment);
// инициализировать
драйвер DIGPAK
extern void far cdecl DeInitDP (short segment);
// выгрузить драйвер DIGPAK

Запись в последовательный порт

Нам осталось сделать функцию, которая могла бы записывать символы в последовательный порт. Для выполнения этого достаточно записать данные в регистр поддержки передачи. Однако мы должны сделать так, чтобы одновременно выполнялись два условия:

Во-первых, ISR не может быть активен;

§ Во-вторых, регистр поддержки передачи должен быть пуст.

Первое условие выполняется как само собой разумеющееся. Однако второе должно быть проверено с помощью пятого бита регистра состояния линии. Если этот бит установлен, передатчик пуст и мы можем послать в порт следующий символ.

Листинг 14.3 содержит программу для передачи символа.

Листинг 14.3. Функция

Serial_Write.

Serial_Write(char ch)

{

// эта функция записывает символ в буфер последовательного порта,

// но вначале она ожидает, пока он освободится

// примечание: эта функция не связана с прерываниями

// и запрещает их на время работы

// ждем, освобождения буфера

while(!(_inp(open_port + SER_LSR) & 0х20)){}

// запрещаем прерывания

_asm cli

// записываем символ в порт

_outp(open_port + SER_THR, ch);

// разрешаем прерывания снова

_asm sti

} // конец функции

Обратите внимание на одну хитрость, примененную в функции Serial_Write:

она запрещает прерывания перед записью символа в порт и затем вновь разрешает их.

Завтрак с Толстяком - музыка в программах

Я попросил моего друга, Джорджа Алистара Зангера, известного под псевдонимом Толстяк, порассуждать о том, как, когда и почему музыка должна использоваться в программах. Толстяк — популярный композитор, предоставляющий широкий диапазон услуг в индустрии мультимедиа.

Толстяк создает музыку в своем доме в Остине, штат Техас для клиентов от Лос-Анджелеса до Нью-Йорка и Гонконга. Среди его клиентов Warner/Elektra/Atlantic, Cannon Films и Southwest Airlines. Он участвовал в создании музыкального оформления для десятка программных продуктов, включая Wing Commander фирмы Origin Systems, The 7th Guest фирмы Virgm/Trilobyte и SSN-21 Seawolf фирмы Electronic Arts.

ЗВУКОВЫЕ ЭФФЕКТЫ И МУЗЫКА

Игры без звука подобны бассейну без воды. Это просто нонсенс! Звук тесно связан с действиями, происходящими в игре. Звуковые эффекты и музыка - это основа магии игр. Они могут изобразить чувство страха, волнения и неприязни. Я считаю, что хороший звук намного важнее хорошей графики. Потому что даже прекрасная, замечательно работающая в реальном времени, трехмерная графика с трассированным пространством без звука превращаетсяпросто в двигающиеся картинки. В этой главе мы узнаем, что же такое Звук и как его реализовать на персональном компьютере. Мы ограничимся звуковой картой Sound Blaster фирмы Creative Labs и совместимыми с ней устройствами. В этой главе мы рассмотрим:

Основы звука;

§ Устройство и архитектуру звуковой карты Sound Blaster;

§ Создание и воспроизведение оцифрованных звуковых эффектов;

§ Частотный синтез звука;

§ MIDI-музыку;

§ Специальные методы работы со звуком.

§ Основы звука

Со звуком мы сталкиваемся каждый день. Это одно из понятий, определить которое не очень тяжело. Звук - это человеческое восприятие волн давления, распространяющихся в воздушной среде, точно так же, как свет - восприятие электромагнитных волн, распространяющихся в пространстве. Вокруг звучащего объекта воздух расширяется и сжимается. Это расширение и сжатие порождает волны, которые, в конце концов, и достигают вашего уха, создавая переменное давление на барабанные перепонки. На рисунке 9.1 изображен источник звука и распространение звуковых волн от него.

Распространение звуковых волн из одной точки в другую по воздуху является механическим, так как оно происходит за счет передачи молекулами воздуха своей кинетической энергии друг другу. Когда волна распространяется, она теряет свою энергию из-за трения (мы воспринимаем это как снижение уровня громкости) до тех пор, пока, наконец, ее энергия окончательно не поглотится воздухом.

Звуковые волны имеют некоторые интересные свойства. Например, известный эффект Доплера. Все мы знаем разницу между звуком приближающегося и удаляющегося поезда. Данный эффект обусловлен тем, что скорость распространения звуковых волн зависит от скорости самого поезда. Не забывайте, что в отличие от световых волн, звук распространяется медленно. В среднем их скорость составляет 600 миль в час, так что поезд, двигающийся со скоростью 60 миль в час, может в достаточной степени повлиять на распространение звука. Если вы вспомните, звук приближающегося поезда выше и его тон (или частота колебаний) постепенно возрастает. После того как поезд прошел, тон (частота) снижается. Все это происходит из-за того, что передвигающийся объект порождает фронт звуковой волны в результате локального повышения давления. Таким образом, поезд одновременно и передвигается, и порождает звук, вследствие чего частота звука приближающегося и удаляющегося поезда различаются.

Теперь поговорим о специфических терминах, которые мы будем использовать при рассмотрении различных звуковых эффектов. Для наглядного представления звуков обычно используют двухмерные графики (см. рис. 9.2).

По оси Х обычно откладывают время, а по оси Y — амплитуду звука. Чистая нота ДО первой октавы (440Гц) будет выглядеть так, как это показано на рисунке 9.3.

Как вы можете видеть, волна порождает сама себя снова и снова и внешне выглядит как функция от времени. Это одно из свойств чистого тона; он может быть описан функцией синуса. Математически это записывается так:

F(t)=sin(2*Pi*F*t)

где F — генерируемая нами частота.

Как легко увидеть на рисунке 9.3, из формы волны мы можем получить несколько параметров. Один из них - амплитуда

(или, проще говоря, уровень громкости). Ее обычно измеряют в децибелах. Децибелы изменяются по логарифмической шкале: звук в 5дБ в 10 раз сильнее звука в 4дБ. (По такой же шкале измеряют силу землетрясения. При 5 баллах лишь немного подрагивает, а при 7 уже рушатся горы, ведь такое землетрясение в 100 раз сильнее!)

Другая величина, определяемая по графику, — это длина звуковой волны. Длина волны определяется, как время или расстояние между двумя вершинами синусоиды. Легко видеть что это длительность одного полного цикла звука. Посмотрите для примера на рисунок 9.4. Здесь изображены два разных волновых графика.

Частота одной волны - 500Гц, а другой - 1000Гц. Тысячегерцовая волна имеет в два раза больше полных циклов за единицу времени, чем пятисотгерцовая.

Теперь мы должны поговорить о частотной характеристике восприятия (frequency response). Обычно человек воспринимает звук, как показано на рисунке 9.5.

Мы слышим в диапазоне 20Гц-15КГц, и восприимчивость обычно сильно падает к 20КГц (большинство людей вообще не воспринимает звук за этим порогом). Следовательно, мы должны создавать наше звуковое сопровождение игры именно в таких пределах.

Достаточно о том, что такое звук. Попробуем его сделать!

Звуковые редакторы

Существуют две разновидности звуков в видеоигре:

§ Синтезированные эффекты;

§ Музыка.

Поскольку синтезированные эффекты пользуются большой популярностью, создано немало инструментальных средств, позволяющих получать интересные звуковые эффекты. Существуют даже CD с сотнями готовых звуковых эффектов: взрывами, шумом автомобилей, ракет и т. д. Однако если CD или библиотека синтезированных звуков вам недоступна, вы сможете сделать немало удивительных открытий, создавая акустические эффекты самостоятельно. Полный набор звуков для Net-Tank был сделан с помощью моих собственных голосовых связок!

Другое дело - музыка. Эту область многие программисты оставляют для специалистов: музыка должна писаться музыкантами, а не программистами. Но если вы совмещаете в себе обоих, вам все под силу. Существует множество музыкальных композиций, которые могли бы перекочевать в ваши игры. Однако, я предлагаю взять уже готовые песни или короткие баллады и использовать их как фундамент. Другой подход, который может оказаться вам больше по душе, заключается в том, чтобы использовать музыкальные записи, сделанные с помощью синтезатора, имеющего midi-выход, и закодированные с помощью ПК. Что бы вы ни решили делать, музыка для игры должна иметь собственный темп, а «характер» музыки должен соответствовать каждому уровню и набору обстоятельств. По этим причинам многие программисты заключают контракты с профессиональными музыкантами по поводу написания музыкальной части игры, чтобы данная работа была выполнена с наилучшим качеством. Следовательно, вам может понадобиться приобрести или создать самим достаточно «продвинутый» звуковой драйвер. Однако если вы считаете, что вам не нужны сложные звуковые эффекты, то дигитайзер, несколько музыкальных примеров и определенный творческий настрой дадут нужные результаты.